分析:(1)以D为坐标原点,DA.DC.DD1所在直线,分别作x轴,Y轴,Z轴,分别出各顶点的坐标,及直线FG1的方向向量和平面FEE1的法向量,然后判断两个向量是否共线,即可得到直线FG1⊥平面FEE1是否成立;
(2)分别求出异面直线E1G1与EA的方向向量,然后代入向量夹角公式,即可得到异面直线E1G1与EA所成角的正弦值.
(3)根据棱锥的几何特征及已知条件,我们可以得到VE-AGF=VE-A1GF=VM-A1GF=VM-A1GF,求出四面体的底面积和高,代入棱锥体积公式,即可得到答案.
解答: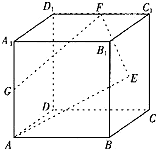
解:(1)证明:以D为坐标原点,DA.DC.DD
1所在直线分别作x轴,Y轴,Z轴,
得E
1(0,2,1),G
1(0,0,1),
又G(2,0,1),F(0,1,2),E(1,2,1),
则
=(0,-1,-1),
=(1,1,-1),
=(0,1,-1),┉┉(2分)
∴
•
=0+(-1)+1=0,
•
=0+(-1)+1=0,即FG
1⊥FE,FG
1⊥FE
1,
又FE
1∩FE=F,∴直线FG
1⊥平面FEE
1(4分)
(2)
=(0,-2,0),
=(1,-2,-1),┉┉(5分)
则
cos<,>=
=
,┉┉(7分)
设异面直线E
1G
1与EA所成角为θ,则sinθ=
=
.┉┉(8分)
(3)∵A.G.A
1,F共面,且G是AA
1的中点,
∴V
E-AGF=V
E-A1GF.┉┉(10分)
取B
1C
1.的中点为M,所以EM∥A
1G,∴EM∥平面A
1GF,
∴V
E-AGF=V
E-A1GF=V
M-A1GF=V
G-A1MF=
×1×=
┉┉(14分)
点评:本题考查的知识点是直线与平面垂直的判定,棱锥的体积,异面直线及其所成的角,建立空间坐标系,将线面关系的判定,及线面夹角问题转化为向量夹角问题是解答本题的关键.

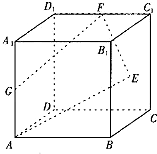 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E是正方形BCC1B1的中心,点F.G分别是棱C1D1,AA1的中点.设点E1,G1分别是点E,G在平面DCC1D1内的正投影.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E是正方形BCC1B1的中心,点F.G分别是棱C1D1,AA1的中点.设点E1,G1分别是点E,G在平面DCC1D1内的正投影. 解:(1)证明:以D为坐标原点,DA.DC.DD1所在直线分别作x轴,Y轴,Z轴,
解:(1)证明:以D为坐标原点,DA.DC.DD1所在直线分别作x轴,Y轴,Z轴,

 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )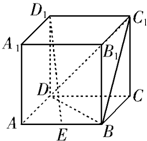 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点. (2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.
(2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.