练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．函数y=x2•（1-3x）在（0，$\frac{1}{3}$）上的最大值是$\frac{1}{12}$．

    分析 由于0＜x＜$\frac{1}{3}$，可得1-3x＞0，变形利用基本不等式可得y=x2（1-3x）即可得出．

    解答 解：∵0＜x＜$\frac{1}{3}$，∴1-3x＞0，
    ∴函数y=x2（1-3x）=$\frac{2}{3}$$•x•x•（\frac{3}{2}-2x）$≤$\frac{2}{3}$•$（\frac{\frac{3}{2}+x+x-2x}{3}）^{3}$=$\frac{1}{12}$，当且仅当x=$\frac{1}{2}$时取等号．
    故答案为：$\frac{1}{12}$．

    点评 本题考查了变形利用基本不等式，考查转化思想的应用，属于基础题．也可以利用导数求解函数的最值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．计算：$\frac{1}{2}{log_2}3\frac{1}{2}{log_9}8$=$\frac{3}{8}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知函数f（x）=x3-3x，则函数h（x）=f[f（x）]-c，c∈[-2，2]的零点个数（　　）
    A．5或6个B．3或9个C．9或10个D．5或9个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．空气污染，又称为大气污染，当空气污染指数（单位：μg/m3）为0～50时，空气质量级别为一级，空气质量
    状况属于优；当空气污染指数为50～100时，空气质量级别为二级，空气质量状况属于良；当空气污染指数为
    100～150时，空气质量级别为三级，空气质量状况属于轻度污染；当空气污染指数为150～200时，空气质量级别为四级，空气质量状况属于中度污染； 2015年1月某日某省x个监测0点数据统计如下：
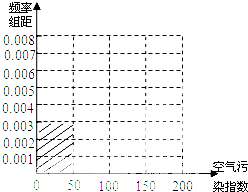
    空气污染指数
    （单位：μg/m3）    		[0，50]（50，100]（100，150]（150，200]
    监测点个数1540y15
    （Ⅰ）根据所给统计表和频率分布直方图中的信息求出x，y的值，并完成频率分布直方图；
    （Ⅱ）统计部门从该省空气质量“良好”和“轻度污染”的两类监测点中采用分层抽样的方式抽取了7个监测点，省环保部门再从中随机选取3个监测点进行调研，记省环保部门“选到空气质量“良好”的城市个数为ξ”，求ξ的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知二阶矩阵A有特征值λ1=3及其对应的一个特征向量$\overrightarrow{a}$1=$[\begin{array}{l}{1}\\{1}\end{array}]$，特征值λ2=-1及其对应的一个特征向量$\overrightarrow{a}$2=$[\begin{array}{l}{1}\\{-1}\end{array}]$，
    （1）求矩阵A；  
    （2）求矩阵A的逆矩阵A-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若函数f（x）=x3-3x-a，当x∈[0，3]上时，m≤f（x）≤n恒成立，则n-m的最小值为（　　）
    A．2B．4C．18D．20

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知偶函数f（x）在[0，+∞）单调递减，f（2）=0．若f（x-1）＞0，求x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．设A={（x，y）|2x+y=7}，B={（x，y）|x+2y=5}，则A∩B=（　　）
    A．{x=3或y=1}B．{3，1}C．{（3，1）}D．（3，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．函数y=$\frac{1}{2}{x}^{2}-lnx$的单调减区间是（　　）
    A．（0，1）B．（0，1）∪（-∞，-1）C．（-∞，1）D．（-∞，+∞）

    查看答案和解析>>

    同步练习册答案