
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| C | 13 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
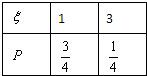
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| C | 36 |
| C | 35 |
| 1 |
| 3 |
| 2 |
| 3 |
| 30×8 |
| 38 |
| 80 |
| 37 |
| 80 |
| 2187 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
在一次电视节目的抢答中,题型为判断题,只有“对”和“错”两种结果,其中某明星判断正确的概率为![]() ,判断错误的概率为
,判断错误的概率为![]() ,若判断正确则加1分,判断错误则减1分,现记“该明星答完
,若判断正确则加1分,判断错误则减1分,现记“该明星答完![]() 题后总得分为
题后总得分为![]() ”. (1)当
”. (1)当![]() 时,记
时,记![]() ,求
,求![]() 的分布列及数学期望及方差;(2)当
的分布列及数学期望及方差;(2)当![]() 时,求
时,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
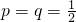 时,记ξ=|S3|,求ξ的分布列及数学期望及方差;
时,记ξ=|S3|,求ξ的分布列及数学期望及方差;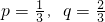 时,求S8=2且Si≥0(i=1,2,3,4)的概率.
时,求S8=2且Si≥0(i=1,2,3,4)的概率.查看答案和解析>>
科目:高中数学 来源:2010年江苏省南通市启东中学高三数学考前辅导材料(2)(解析版) 题型:解答题
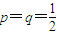 时,记ξ=|S3|,求ξ的分布列及数学期望及方差;
时,记ξ=|S3|,求ξ的分布列及数学期望及方差;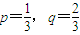 时,求S8=2且Si≥0(i=1,2,3,4)的概率.
时,求S8=2且Si≥0(i=1,2,3,4)的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com