
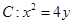 ,直线
,直线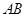 过抛物线
过抛物线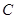 的焦点
的焦点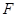 ,交
,交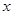 轴于点
轴于点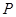 .
.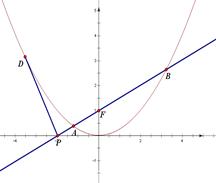
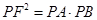 ;
;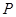 作抛物线
作抛物线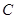 的切线,切点为
的切线,切点为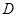 (异于原点),
(异于原点),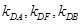 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;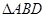 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由. (2) 能 抛物线
(2) 能 抛物线
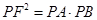 转化为点的坐标关系.
转化为点的坐标关系.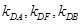 ,结合韦达定理验证
,结合韦达定理验证 是否成立.
是否成立.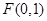 ,所以假设直线AB为
,所以假设直线AB为 ,
, ,所以点
,所以点 .联立
.联立 可得,
可得, ,所以
,所以 .因为
.因为 ,
,
 .所以
.所以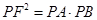 .
. ,
, 的导数为
的导数为 .所以可得
.所以可得 ,即可得
,即可得 .即得
.即得 .
. .
.

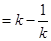 .所以可得
.所以可得 即
即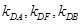 是否恒成等差数列.
是否恒成等差数列. 重心的坐标为
重心的坐标为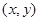 由题意可得
由题意可得 .即
.即 ,
,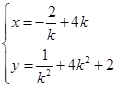 消去k可得
消去k可得 .
.

科目:高中数学 来源:不详 题型:解答题
 (
( )是曲线
)是曲线 上的点,
上的点, ,
, 是数列
是数列 的前
的前 项和,且满足
项和,且满足 ,
, ,
, .
. (
( )是常数数列;
)是常数数列; 的取值集合
的取值集合 ,使
,使 时,数列
时,数列 是单调递增数列;
是单调递增数列; 时,弦
时,弦 (
( )的斜率随
)的斜率随 单调递增
单调递增查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 是各项为不同的正数的等差数列,
是各项为不同的正数的等差数列, 成等差数列,又
成等差数列,又 .
. 为等比数列;
为等比数列; 前3项的和为
前3项的和为 ,求数列
,求数列 的首项和公差;
的首项和公差; 为数列
为数列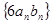 的前
的前 项和,求
项和,求 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com