
【题目】函数f(x)=lnx﹣ax2+x有两个零点,则实数a的取值范围是( )
A.(0,1)
B.(﹣∞,1)
C.(﹣∞, ![]() )
)
D.(0, ![]() )
)
【答案】A
【解析】解:∵函数f(x)=lnx﹣ax2+x有两个不同的零点, 不妨令g(x)=lnx,h(x)=ax2﹣x,
将零点问题转化为两个函数交点的问题;
又函数h(x)=x(ax﹣1),
当a≤0时,g(x)和h(x)只有一个交点,不满足题意;
当a>0时,由lnx﹣ax2+x=0,得a= ![]() ;
;
令r(x)= ![]() ,则r′(x)=
,则r′(x)= ![]() =
= ![]() ,
,
当0<x<1时,r'(x)>0,r(x)是单调增函数,
当x>1时,r'(x)<0,r(x)是单调减函数,且 ![]() >0,∴0<a<1;
>0,∴0<a<1;
或当a>0时,作出两函数g(x)=lnx,h(x)=ax2﹣x的图象,如图所示; 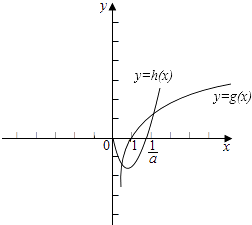
g(x)=lnx交x轴于点(1,0),
h(x)=ax2﹣x交x轴于点(0,0)和点( ![]() ,0);
,0);
要使方程有两个零点,应满足两函数有两个交点,
即 ![]() >1,解得0<a<1;
>1,解得0<a<1;
∴a的取值范围是(0,1).
故选:A.
函数f(x)=lnx﹣ax2+x有两个不同的零点,转化为函数g(x)=lnx和h(x)=ax2﹣x交点的问题;
讨论a≤0时不满足题意,a>0时,求得(a)max=1,当x→+∞时,a→0,从而可得答案.
或a>0时,作出两函数g(x)=lnx,h(x)=ax2﹣x的图象,由 ![]() >1求出a的取值范围.
>1求出a的取值范围.


科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() ,且直线
,且直线![]() 有唯一的一个点
有唯一的一个点![]() ,使得过
,使得过![]() 点作圆
点作圆![]() 的两条切线互相垂直,则
的两条切线互相垂直,则![]() _____;设
_____;设![]() 是直线
是直线![]() 上的一条线段,若对于圆
上的一条线段,若对于圆![]() 上的任意一点
上的任意一点![]() ,则
,则![]() 的最小值_____.
的最小值_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥PB,PC=2. 
(1)求证:平面PAB⊥平面ABCD;
(2)若PA=PB,求二面角A﹣PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(cosθ,sinθ),
=(cosθ,sinθ), ![]() =(﹣
=(﹣ ![]() ,
, ![]() );
);
(1)若 ![]() ∥
∥ ![]() ,且θ∈(0,π),求θ;
,且θ∈(0,π),求θ;
(2)若|3 ![]() +
+ ![]() |=|
|=| ![]() ﹣3
﹣3 ![]() |,求|
|,求| ![]() +
+ ![]() |的值.
|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com