
分析 由f(x)=$\sqrt{(x-1)^{2}+1}$+$\sqrt{(x+1)^{2}+1}$的几何意义:点(x,0)到(1,1)与(-1,1)的距离之和,过B作x轴的对称点D(1,-1),当C与O点重合时,丨AC丨+丨BC丨,取最小值,f(x)min=丨AD丨=$\sqrt{[1-(-1)]^{2}+(-1-1)^{2}}$=2$\sqrt{2}$.
解答 解:由f(x)=$\sqrt{(x-1)^{2}+1}$+$\sqrt{(x+1)^{2}+1}$的几何意义:点(x,0)到(1,1)与(-1,1)的距离之和,
即f(x)表示丨AC丨+丨BC丨,
过B作x轴的对称点D(1,-1),
连接AD,交x轴于O点,
∴当C与O点重合时,丨AC丨+丨BC丨,取最小值,
∴f(x)min=丨AD丨=$\sqrt{[1-(-1)]^{2}+(-1-1)^{2}}$=2$\sqrt{2}$,
函数f(x)=$\sqrt{(x-1)^{2}+1}$+$\sqrt{(x+1)^{2}+1}$的最小值为:2$\sqrt{2}$,
故答案为:2$\sqrt{2}$. \
\
点评 本题考查点到直线的距离公式的几何意义,考查数形结合思想,函数的最值,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
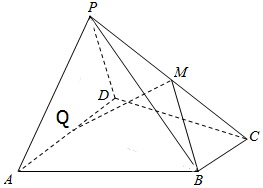 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,M是棱PC的中点,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,M是棱PC的中点,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{4}{3}$,+∞) | B. | (1,$\frac{4}{3}$] | C. | [$\frac{5}{3}$,+∞) | D. | (1,$\frac{5}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2x+2)5 | B. | 2x5 | C. | (2x-1)5 | D. | 32x5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com