练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．已知向量$\overrightarrow a$与$\overrightarrow b$的夹角为120°，且$\overrightarrow a=（-2，-6）$，$|\overrightarrow b|=\sqrt{10}$，则$\overrightarrow a•\overrightarrow b$=-10．

    分析 可先求出$|\overrightarrow{a}|=2\sqrt{10}$，从而根据$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos＜\overrightarrow{a}，\overrightarrow{b}＞$即可求出数量积$\overrightarrow{a}•\overrightarrow{b}$的值．

    解答 解：$|\overrightarrow{a}|=\sqrt{4+36}=2\sqrt{10}$；
    又$|\overrightarrow{b}|=\sqrt{10}，＜\overrightarrow{a}，\overrightarrow{b}＞=120°$；
    ∴$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos120°$=$2\sqrt{10}×\sqrt{10}×（-\frac{1}{2}）=-10$．
    故答案为：-10．

    点评 考查根据向量坐标求向量长度的方法，以及数量积的计算公式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    20．（1）已知$f（\frac{1}{x}）=\frac{x}{{1-{x^2}}}$，求函数f（x）的解析式．
    （2）已知二次函数f（x）满足f（0）=2，f（x+1）-f（x）=2x-1对任意实数x都成立，求函数f（x）的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

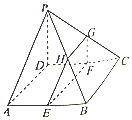    12．如图，在四棱锥P-ABCD中，PD⊥平面ABCD，底面ABCD为菱形，．点分E，F，G，H别是棱AB，CD，PC，PB上共面的四点，且BC∥EF． 
    证明：GH∥EF．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

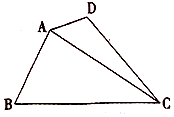    9．如图，四边形ABCD中，∠BAD=135°，∠ADC=120°，∠BCD=45°，∠ABC=60°，BC=$\sqrt{3}$，则线段AC长度的取值范围是（　　）
    A．$[{\sqrt{2}，\sqrt{3}}）$B．$[{\frac{3}{2}，\sqrt{3}}）$C．$（{\sqrt{2}，\sqrt{3}}）$D．$（{\frac{3}{2}，\sqrt{3}}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知命题p：?x∈（1，+∞），log2x＜log3x；命题q：?x∈（0，+∞），2-x=lnx．则下列命题中为真命题的是（　　）
    A．p∧qB．（￢p）∧qC．p∧（￢q）D．（￢p）∧（￢q）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．定义两种运算：a⊕b=$\sqrt{{a}^{2}-{b}^{2}}$，a?b=$\sqrt{（a-b）^{2}}$，则f（x）=$\frac{2⊕x}{2-（x?2）}$是（　　）
    A．奇函数B．偶函数C．既奇又偶函数D．非奇非偶函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．若集合{1，$\frac{b}{a}$，a}={0，a+b，a2}，则a2+b3=（　　）
    A．-1B．1C．0D．±1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知定义在[-3，3]上的函数y=f（x）是增函数．
    （1）若f（m+1）-f（2m-1）＞0，求m的取值范围；
    （2）若函数f（x）是奇函数，且f（2）=1，解不等式f（x+1）+1＞0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．在△ABC中，内角A，B，C所对的边分别为a，b，c，已知$acosC+\sqrt{3}asinC-b-c=0$．
    （1）求角A的大小；
    （2）若a=7，b+c=11，求△ABC的面积．

    查看答案和解析>>

    同步练习册答案