
【题目】某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧 ![]() 、
、 ![]() 所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).
所在圆的半径分别为f(x)、R米,圆心角为θ(弧度). 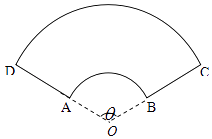
(1)若θ= ![]() ,r1=3,r2=6,求花坛的面积;
,r1=3,r2=6,求花坛的面积;
(2)设计时需要考虑花坛边缘(实线部分)的装饰问题,已知直线部分的装饰费用为60元/米,弧线部分的装饰费用为90元/米,预算费用总计1200元,问线段AD的长度为多少时,花坛的面积最大?
【答案】
(1)解:设花坛的面积为S平方米. ![]()
= ![]() =
= ![]()
答:花坛的面积为 ![]() ;
;
(2)解: ![]() 的长为r1θ米,
的长为r1θ米, ![]() 的长为r2θ米,线段AD的长为(r2﹣r1)米
的长为r2θ米,线段AD的长为(r2﹣r1)米
由题意知602(r2﹣r1)+90(r1θ+r2θ)=1200
即4(r2﹣r1)+3(r2θ+r1θ)=40*
![]()
由*式知, ![]()
记r2﹣r1=x,则0<x<10
所以 ![]() =
= ![]()
当x=5时,S取得最大值,即r2﹣r1=5时,花坛的面积最大.
答:当线段AD的长为5米时,花坛的面积最大.
【解析】(1)设花坛的面积为S平方米. ![]() ,即可得出结论;(2)记r2﹣r1=x,则0<x<10,所以
,即可得出结论;(2)记r2﹣r1=x,则0<x<10,所以 ![]() =
= ![]() ,即可得出结论.
,即可得出结论.
【考点精析】解答此题的关键在于理解扇形面积公式的相关知识,掌握若扇形的圆心角为![]() ,半径为
,半径为![]() ,弧长为
,弧长为![]() ,周长为
,周长为![]() ,面积为
,面积为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,过E点做EF⊥PB交PB于点F.求证: 
(1)PA∥平面DEB;
(2)PB⊥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,体积为 ![]() ,底面是边长为
,底面是边长为 ![]() 的正三角形,若P为底面A1B1C1的中心,则PA与平面A1B1C1所成角的大小为( )
的正三角形,若P为底面A1B1C1的中心,则PA与平面A1B1C1所成角的大小为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点. 
(1)求证:AF⊥EF;
(2)求二面角A﹣PC﹣B的平面角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)的图象关于点(1,0)对称,且当x∈[1,2]时,f(x)=﹣2x+2,若函数y=f(x)﹣loga(|x|+1)恰好有8个零点,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2 的正方体ABCD﹣A1B1C1D1中,M是A1B1的中点,点P是侧面CDD1C1上的动点,且MP∥截面AB1C,则线段MP长度的取值范围是( )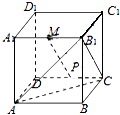
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,其中0<ω<2; (Ⅰ)若f(x)的最小正周期为π,求f(x)的单调增区间;
,其中0<ω<2; (Ⅰ)若f(x)的最小正周期为π,求f(x)的单调增区间;
(Ⅱ)若函数f(x)的图象的一条对称轴为 ![]() ,求ω的值.
,求ω的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在三棱柱ABC﹣A1B1C1中,已知AB⊥侧面BB1C1C,BC= ![]() ,AB=CC1=2,∠BCC1=
,AB=CC1=2,∠BCC1= ![]() ,点E在棱BB1上.
,点E在棱BB1上. 
(1)求C1B的长,并证明C1B⊥平面ABC;
(2)若BE=λBB1 , 试确定λ的值,使得二面角A﹣C1E﹣C的余弦值为 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com