
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 求导f′(x)=1-x+x2-x3+…+x2014-x2015,分类讨论以确定f(x)的单调性,从而确定函数的极值的正负,从而利用函数的零点判定定理判断即可.
解答 解:∵f(x)=1+x-$\frac{{x}^{2}}{2}$+$\frac{{x}^{3}}{3}$-$\frac{{x}^{4}}{4}$+…+$\frac{{x}^{2015}}{2015}$-$\frac{{x}^{2016}}{2016}$,
∴f′(x)=1-x+x2-x3+…+x2014-x2015,
当x=-1时,f′(x)=2016>0,
当x≠-1时,f′(x)=$\frac{1-{x}^{2016}}{1+x}$,
故当-2<x<-1或-1<x<1时,f′(x)>0;
当1<x<2时,f′(x)<0;
故f(x)在[-2,1]上单调递增,在(1,2]上单调递减,
又∵f(-2)<0,f(1)>0,f(2)<0,
∴f(x)在(-2,1)和(1,2)内各有一个零点,
故选:B.
点评 本题考查了导数的综合应用及分类讨论的思想应用,同时考查了零点的判定定理的应用.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
| A. | y=-x2 | B. | $y={(\frac{1}{π})^x}$ | C. | $y={log_{\frac{1}{2}}}x$ | D. | $y=\sqrt{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
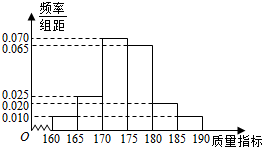 从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.
从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥-1} | B. | {x|x<3} | C. | {x|-1<x<3} | D. | {x|-1≤x<3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com