
【题目】如图,在四棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 为直角梯形,其中
为直角梯形,其中![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
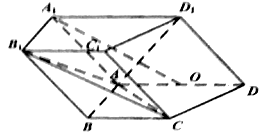
(1)求证:![]() 平面
平面![]() ;
;
(2)求锐二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接![]() ,证明四边形
,证明四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,所以
,所以![]() 平面
平面![]() ;(2)以
;(2)以![]() 为原点,所
为原点,所![]() 在直线分别为
在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立坐标系,利用两个半平面的法向量求得二面角的余弦值为
轴建立坐标系,利用两个半平面的法向量求得二面角的余弦值为![]() .
.
试题解析:
(1)证明:
如图,连接![]() ,则四边形
,则四边形![]() 为正方形,所以
为正方形,所以![]() ,且
,且![]() ,....2分
,....2分
故四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
又![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ...............5分
...............5分
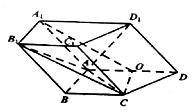
(2)因为![]() 为
为![]() 的中点,所以
的中点,所以![]() ,又侧面
,又侧面![]() 底面
底面![]() ,
,
交线为![]() ,故
,故![]() 底面
底面![]() .........................6分
.........................6分
以![]() 为原点,所
为原点,所![]() 在直线分别为
在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的坐标系,
轴建立如图所示的坐标系,
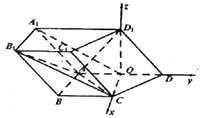
则![]() ,
,
∴![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,由
的一个法向量,由![]() ,得
,得![]() ,
,
令![]() ,则
,则![]() ,∴
,∴![]() .
.
又设![]() 为平面
为平面![]() 的一个法向量,由
的一个法向量,由![]() ,得
,得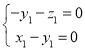 ,令
,令![]() ,
,
则![]() ,∴
,∴![]() ,.............9分
,.............9分
则![]() ,故所求锐二面角
,故所求锐二面角![]() 的余弦值为
的余弦值为![]() .........12分
.........12分
注:第2问用几何法做的酌情给分.


科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 |
|
|
|
|
|
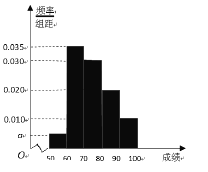
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取
年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取![]() 名学生的数学成绩进行统计,将他们的成绩分成六段
名学生的数学成绩进行统计,将他们的成绩分成六段![]() 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.

(1)求这40名学生中数学成绩不低于120分的学生人数;
(2)若从数学成绩![]() 内的学生中任意抽取2人,求成绩在
内的学生中任意抽取2人,求成绩在![]() 中至少有一人的概率.
中至少有一人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应国家号召,某地决定分批建设保障性住房供给社会.首批计划用100万元购得一块土地,该土地可以建造每层1 000平方米的楼房,楼房的每平方米建筑费用与建筑高度有关,楼房每升高一层,整层楼每平方米建筑费用提高20元.已知建筑第5层楼房时,每平方米建筑费用为800元.
(1)若建筑第x层楼时,该楼房综合费用为y万元(综合费用是建筑费用与购地费用之和),写出y=f(x)的表达式;
(2)为了使该楼房每平方米的平均综合费用最低,应把楼层建成几层?此时平均综合费用为每平方米多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出![]() 盒该产品获利润
盒该产品获利润![]() 元;未售出的产品,每盒亏损
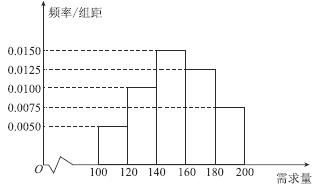
元;未售出的产品,每盒亏损![]() 元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了
元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了![]() 盒该产品,以
盒该产品,以![]() (单位:盒,
(单位:盒, ![]() )表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.
)表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.
(1)根据直方图估计这个开学季内市场需求量![]() 的中位数;
的中位数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (x≥0)成等差数列.又数列{an}(an>0)中,a1=3 ,此数列的前n项的和Sn(n∈N*)对所有大于1的正整数n都有Sn=f(Sn-1).
(x≥0)成等差数列.又数列{an}(an>0)中,a1=3 ,此数列的前n项的和Sn(n∈N*)对所有大于1的正整数n都有Sn=f(Sn-1).
(1)求数列{an}的第n+1项;
(2)若![]() 是
是![]() ,
,![]() 的等比中项,且Tn为{bn}的前n项和,求Tn.
的等比中项,且Tn为{bn}的前n项和,求Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面α⊥平面β,α∩β=n,直线lα,直线mβ,则下列说法正确的个数是( )
①若l⊥n,l⊥m,则l⊥β;②若l∥n,则l∥β;③若m⊥n,l⊥m,则m⊥α.
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com