
【题目】为了解高中学生对数学课是否喜爱是否和性别有关,随机调查220名高中学生,将他们的意见进行了统计,得到如下的![]() 列联表.
列联表.
喜爱数学课 | 不喜爱数学课 | 合计 | |
男生 | 90 | 20 | 110 |
女生 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断,能否有![]() 的把握认为“喜爱数学课与性别”有关;
的把握认为“喜爱数学课与性别”有关;
(2)为培养学习兴趣,从不喜爱数学课的学生中进行进一步了解,从上述调查的不喜爱数学课的人员中按分层抽样抽取6人,再从这6人中随机抽出2名进行电话回访,求抽到的2人中至少有1名“男生”的概率.
参考公式: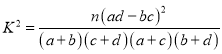 .
.
P( | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为准确把握市场规律,某公司对其所属商品售价进行市场调查和模型分析,发现该商品一年内每件的售价按月近似呈![]() 的模型波动(
的模型波动(![]() 为月份),已知3月份每件售价达到最高90元,直到7月份每件售价变为最低50元.则根据模型可知在10月份每件售价约为_____.(结果保留整数)
为月份),已知3月份每件售价达到最高90元,直到7月份每件售价变为最低50元.则根据模型可知在10月份每件售价约为_____.(结果保留整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保护环境,某工厂在国家的号召下,把废弃物回收转化为某种产品,经测算,处理成本![]() (万元)与处理量
(万元)与处理量![]() (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为:
![]() ,且每处理一吨废弃物可得价值为
,且每处理一吨废弃物可得价值为![]() 万元的某种产品,同时获得国家补贴
万元的某种产品,同时获得国家补贴![]() 万元.
万元.
(1)当![]() 时,判断该项举措能否获利?如果能获利,求出最大利润;
时,判断该项举措能否获利?如果能获利,求出最大利润;
如果不能获利,请求出国家最少补贴多少万元,该工厂才不会亏损?
(2)当处理量为多少吨时,每吨的平均处理成本最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线l的参数方程是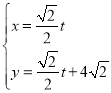 (t为参数),以O为极点,x轴正半轴为极轴的极坐标系中,圆C的极坐标方程为
(t为参数),以O为极点,x轴正半轴为极轴的极坐标系中,圆C的极坐标方程为![]() .
.
(1)求直线l的普通方程和圆C的直角坐标方程;
(2)由直线l上的点向圆C引切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,四边形ABCD为平行四边形,BD⊥DC,△PCD为正三角形,平面PCD⊥平面ABCD,E为PC的中点.
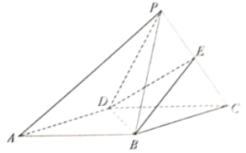
(1)证明:AP∥平面EBD;
(2)证明:BE⊥PC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动.现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
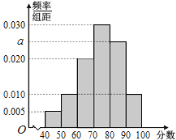
(1)求![]() 的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(2)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点P(4,0)的动直线与抛物线C:![]() 交于点A,B,且
交于点A,B,且![]() (点O为坐标原点).
(点O为坐标原点).
(1)求抛物线C的方程;
(2)当直线AB变动时,x轴上是否存在点Q使得点P到直线AQ,BQ的距离相等,若存在,求出点Q坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com