
【题目】已知函数 ![]()
(1)判断f(x)的奇偶性并证明;
(2)若f(x)的定义域为[α,β](β>α>0),判断f(x)在定义域上的增减性,并加以证明;
(3)若0<m<1,使f(x)的值域为[logmm(β﹣1),logmm(α﹣1)]的定义域区间[α,β](β>α>0)是否存在?若存在,求出[α,β],若不存在,请说明理由.
【答案】
(1)解:由 ![]() 得f(x)的定义域为(﹣∞,﹣3)∪(3,+∞),关于原点对称.
得f(x)的定义域为(﹣∞,﹣3)∪(3,+∞),关于原点对称.
∵ ![]()
∴f(x)为奇函数
(2)解:∵f(x)的定义域为[α,β](β>α>0),则[α,β](3,+∞).
设x1,x2∈[α,β],则x1<x2,且x1,x2>3,
f(x1)﹣f(x2)= ![]() =
= ![]()
∵(x1﹣3)(x2+3)﹣(x1+3)(x2﹣3)=6(x1﹣x2)<0,
∴(x1﹣3)(x2+3)<(x1+3)(x2﹣3)
即 ![]() ,
,
∴当0<m<1时,logm ![]() ,即f(x1)>f(x2);
,即f(x1)>f(x2);
当m>1时,logm ![]() ,即f(x1)<f(x2),
,即f(x1)<f(x2),
故当0<m<1时,f(x)为减函数;m>1时,f(x)为增函数.
(3)解:由(1)得,当0<m<1时,f(x)在[α,β]为递减函数,
∴若存在定义域[α,β](β>α>0),使值域为[logmm(β﹣1),logmm(α﹣1)],
则有 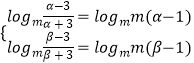
∴ 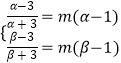
∴α,β是方程 ![]() 的两个解
的两个解
解得当 ![]() 时,[α,β]=
时,[α,β]= ![]() ,
,
当 ![]() 时,方程组无解,即[α,β]不存在.
时,方程组无解,即[α,β]不存在.
【解析】(1)先求得f(x)的定义域为(﹣∞,﹣3)∪(3,+∞),关于原点对称.再验证 ![]() ,从而可得f(x)为奇函数;(2)f(x)的定义域为[α,β](β>α>0),则[α,β](3,+∞).设x1 , x2∈[α,β],则x1<x2 , 且x1 , x2>3,作差f(x1)﹣f(x2)=
,从而可得f(x)为奇函数;(2)f(x)的定义域为[α,β](β>α>0),则[α,β](3,+∞).设x1 , x2∈[α,β],则x1<x2 , 且x1 , x2>3,作差f(x1)﹣f(x2)= ![]() =
= ![]() ,从而可知当0<m<1时,logm
,从而可知当0<m<1时,logm ![]() ,即f(x1)>f(x2);当m>1时,logm
,即f(x1)>f(x2);当m>1时,logm ![]() ,即f(x1)<f(x2),故当0<m<1时,f(x)为减函数;m>1时,f(x)为增函数.(3)由(1)得,当0<m<1时,f(x)在[α,β]为递减函数,故若存在定义域[α,β](β>α>0),使值域为[logmm(β﹣1),logmm(α﹣1)],则有
,即f(x1)<f(x2),故当0<m<1时,f(x)为减函数;m>1时,f(x)为增函数.(3)由(1)得,当0<m<1时,f(x)在[α,β]为递减函数,故若存在定义域[α,β](β>α>0),使值域为[logmm(β﹣1),logmm(α﹣1)],则有 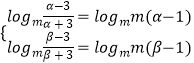 ,从而问题可转化为α,β是方程
,从而问题可转化为α,β是方程 ![]() 的两个解,进而问题得解.
的两个解,进而问题得解.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大? 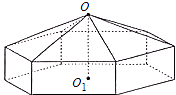
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin (2x+ ![]() ).
).
(1)求函数f(x)的最小正周期及其单调减区间;
(2)用“五点法”画出函数g(x)=f(x),x∈[﹣ ![]() ,
, ![]() ]的图象(完成列表格并作图),由图象研究并写出g(x)的对称轴和对称中心.
]的图象(完成列表格并作图),由图象研究并写出g(x)的对称轴和对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的二次函数f(x)=ax2﹣4bx+1. (Ⅰ)设集合A={﹣1,1,2,3,4,5}和B={﹣2,﹣1,1,2,3,4},分别从集合A,B中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率.
(Ⅱ)设点(a,b)是区域 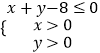 内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女子善织,日益功,疾,初日织五尺,今一月织九匹三丈(1匹=40尺,一丈=10尺),问日益几何?”其意思为:“有一女子擅长织布,每天比前一天更加用功,织布的速度也越来越快,从第二天起,每天比前一天多织相同量的布,第一天织5尺,一月织了九匹三丈,问每天增加多少尺布?”若一个月按30天算,则每天增加量为( ) 
A.![]() 尺
尺
B.![]() 尺
尺
C.![]() 尺
尺
D.![]() 尺
尺
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com