
【题目】如图1,在直角梯形![]() 中,
中,![]() ,
,![]() ,且
,且![]() .现以
.现以![]() 为一边向形外作正方形
为一边向形外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使平面
翻折,使平面![]() 与平面
与平面![]() 垂直,
垂直,![]() 为
为![]() 的中点,如图2.
的中点,如图2.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)取EC中点N,连接MN,BN,证明BN∥AM.说明BN平面BEC,且AM平面BEC,即可证明AM∥平面BEC;
(2)先证明ED⊥BC,BC⊥BD,ED∩BD=D,即可证明BC⊥平面BDE;
(3)利用VE-BCD=VD-BCE,求出底面DCB的面积,高为DE,即可求三棱锥D-BCE的体积.
证明:取![]() 中点
中点![]() ,连结
,连结![]() .
.

在△![]() 中,
中,![]() 分别为
分别为![]() 的中点,
的中点,
所以![]() ∥
∥![]() ,且
,且![]() .
.
由已知![]() ∥
∥![]() ,
,![]() , 所以
, 所以![]() ∥
∥![]() ,且
,且![]() .
.
又因为![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() , 所以
, 所以![]() ∥平面
∥平面![]() .
.
(2)证明:在正方形![]() 中,
中,![]() .
.
又因为平面![]()
![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() .
.
在直角梯形![]() 中,
中,![]() ,
,![]() ,可得
,可得![]() .
.
在△![]() 中,
中,![]() , 所以
, 所以![]() .
.
所以![]() , 所以
, 所以![]() 平面
平面![]() .
.
(3)由(2)知,![]() ,
,
所以![]()
又因为![]() 平面
平面![]() ,所以
,所以![]() =
=


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 和
和![]() 是全等的等腰梯形,其中
是全等的等腰梯形,其中![]() ,且
,且![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 是
是![]() 的中点.
的中点.
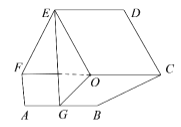
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)请在图中所给的点中找出两个点,使得这两点所在的直线与平面![]() 垂直,并给出证明;
垂直,并给出证明;
(Ⅲ)在线段![]() 上是否存在点,使得
上是否存在点,使得![]() 平面
平面![]() ?如果存在,求出
?如果存在,求出![]() 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了![]() 人,回答问题计结果如下图表所示:
人,回答问题计结果如下图表所示:

(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆方程;
(2)设不过原点![]() 的直线
的直线![]() ,与该椭圆交于
,与该椭圆交于![]() 两点,直线
两点,直线![]() 的斜率依次为
的斜率依次为![]() ,满足
,满足![]() ,试问:当
,试问:当![]() 变化时,
变化时,![]() 是否为定值?若是,求出此定值,并证明你的结论;若不是请说明理由.
是否为定值?若是,求出此定值,并证明你的结论;若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知菱形ABCD如图(1)所示,其中∠ACD=60°,AB=2,AC与BD相交于点O,现沿AC进行翻折,使得平面ACD⊥平面ABC,取点E,连接AE,BE,CE,DE,使得线段BE再平面ABC内的投影落在线段OB上,得到的图形如图(2)所示,其中∠OBE=60°,BE=2. 
(Ⅰ)证明:DE⊥AC;
(Ⅱ)求二面角A﹣BE﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com