
根据正弦函数的图像,写出使不等式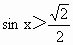 (xÎR)成立的角x的取值范围.
(xÎR)成立的角x的取值范围.
科目:高中数学 来源:设计必修四数学北师版 北师版 题型:044
某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下面是水深数据:
据上述数据描成的曲线如图所示,经拟合,该曲线可近似地看成正弦函数y=Asinωx+b的图像.

(1)试根据数据表和曲线,求出y=Asinωx+b的表达式;
(2)一般情况下,船舶航行时船底与海底的距离不小于4.5米是安全的,如果某船的吃水深度(船底与水面的距离)为7米,那么该船在什么时间段能够安全进港?若该船欲当天安全离港,它在港内停留的时间最多不能超过多长时间(忽略离港所用的时间)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com