
【题目】运行如下程序框图,如果输入的t∈[0,5],则输出S属于( ) 
A.[﹣4,10)
B.[﹣5,2]
C.[﹣4,3]
D.[﹣2,5]
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共 ![]() 个,生产一个卫兵需
个,生产一个卫兵需 ![]() 分钟,生产一个骑兵需
分钟,生产一个骑兵需 ![]() 分钟,生产一个伞兵需
分钟,生产一个伞兵需 ![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过 ![]() 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润 ![]() 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润 ![]() 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润 ![]() 元.
元.
(1)用每天生产的卫兵个数 ![]() 与骑兵个数
与骑兵个数 ![]() 表示每天的利润
表示每天的利润 ![]() (元);
(元);
(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了考查两个变量![]() 和
和![]() 之间的线性关系,甲、乙两位同学各自独立作了
之间的线性关系,甲、乙两位同学各自独立作了![]() 次和
次和![]() 次试验,并且利用线性回归方法,求得回归直线分别为
次试验,并且利用线性回归方法,求得回归直线分别为![]() 、
、![]() ,已知两人得的试验数据中,变量
,已知两人得的试验数据中,变量![]() 和
和![]() 的数据的平均值都相等,且分别都是
的数据的平均值都相等,且分别都是![]() 、
、![]() ,那么下列说法正确的是( )
,那么下列说法正确的是( )
A. 直线![]() 和
和![]() 一定有公共点
一定有公共点![]() B. 必有直线
B. 必有直线![]()
C. 直线![]() 和
和![]() 相交,但交点不一定是
相交,但交点不一定是![]() D.
D. ![]() 和
和![]() 必定重合
必定重合
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,且将全班![]() 人的成绩记为
人的成绩记为![]() 由右边的程序运行后,输出
由右边的程序运行后,输出![]() .据此解答如下问题:
.据此解答如下问题:
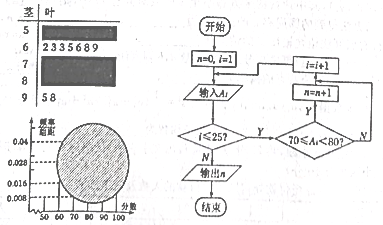
注:图中![]() 表示“是”,
表示“是”,![]() 表示“否”
表示“否”
(1)求茎叶图中破损处分数在![]() ,
,![]() ,
,![]() 各区间段的频数;
各区间段的频数;
(2)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣x2﹣lnx存在极值,若这些极值的和大于5+ln2,则实数a的取值范围为( )
A.(﹣∞,4)
B.(4,+∞)
C.(﹣∞,2)
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱锥C﹣ABDE中,DB⊥平面ABC,AE∥DB,△ABC是边长为2的等边三角形,AE=1,M为AB的中点. 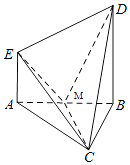
(1)求证:CM⊥EM;
(2)若直线DM与平面ABC所成角的正切值为2,求二面角B﹣CD﹣E的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从万州二中高二年级文科学生中随机抽取60名学生,将其月考的政治成绩(均为整数)分成六段:![]() 后得到如下频率分布直方图.
后得到如下频率分布直方图.
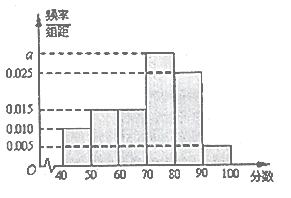
(1)求分数在![]() 内的频率;
内的频率;
(2)用分层抽样的方法在80分以上(含 80分)的学生中抽取一个容量为6的样本, 从该样本中任意选取2人,求其中恰有1 人的分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其函数图象的相邻两条对称轴之间的距离为
,其函数图象的相邻两条对称轴之间的距离为![]() .
.
(1)求函数![]() 的解析式及对称中心;
的解析式及对称中心;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度得到函数
个单位长度得到函数![]() 的图象,若关于
的图象,若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实根,求实数
上有两个不相等的实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com