
(12分)已知函数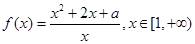
(Ⅰ)当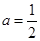 时,求函数
时,求函数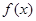 的最小值;
的最小值;
(Ⅱ)若对任意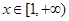 ,
,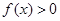 恒成立,试求实数
恒成立,试求实数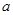 的取值范围.
的取值范围.
(Ⅰ) 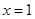 时,
时,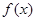 取得最小值
取得最小值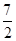 .(Ⅱ)
.(Ⅱ) 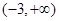 .
.
【解析】
试题分析:(1)先将原式化成求解导数f‘(x),再利用导数的正负与函数单调性的关系,即可求得函数f(x)的最小值;
(2)原题等价于x2+2x+a>0对x∈[1,+∞)恒成立,再结合二次函数的单调性只须g(1)>0,从而求得实数a的取值范围;
解(Ⅰ) 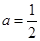 时,
时,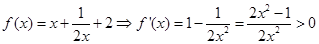 (因为
(因为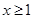 )
)
所以,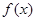 在
在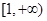 上单调递增,故
上单调递增,故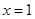 时,
时,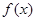 取得最小值
取得最小值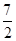 .
.
(Ⅱ) 因为对任意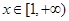 ,
,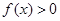 恒成立,即
恒成立,即 恒成立,只需
恒成立,只需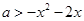 恒成立,只需
恒成立,只需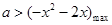 ,因为
,因为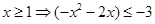 ,
,
所以,实数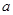 的取值范围是
的取值范围是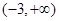 .
.
考点:本题主要考查了函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
点评:解决该试题的关键是是对于同一个问题的不同的处理角度,可以运用均值不等式得到最值,也可以结合导数的工具得到最值,对于恒成立问题一般都是转换为求解函数的 最值即可得到。


科目:高中数学 来源:2011届广东省深圳高级中学高三高考最后模拟考试文数 题型:解答题
(本小题满分14分)已知函数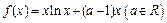 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(Ⅱ)求函数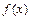 在区间
在区间 上的最小值;
上的最小值;
(Ⅲ)若关于的方程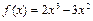 在区间
在区间 内有两个不相等的实数根,求实数a的取值范围.
内有两个不相等的实数根,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省天水市高三第三次考试文科数学试卷(解析版) 题型:解答题
(本小题10分)已知函数 当
当 时,求不等式
时,求不等式 的解集;若
的解集;若 的解集包含
的解集包含 ,求a的取值范围。
,求a的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com