
【题目】在平面直角坐标系 xOy 中,已知椭圆 C:![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,且过点
,且过点![]() ,点P在第四象限, A为左顶点, B为上顶点, PA交y轴于点C,PB交x轴于点D.
,点P在第四象限, A为左顶点, B为上顶点, PA交y轴于点C,PB交x轴于点D.
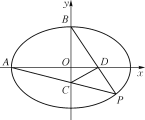
(1) 求椭圆 C 的标准方程;
(2) 求 △PCD 面积的最大值.
【答案】(1)![]() +y2=1;(2)
+y2=1;(2)![]() -1
-1
【解析】
(1)由离心率![]() ,再把点
,再把点![]() 坐标代入
坐标代入![]() =1,结合
=1,结合![]() 可求得
可求得![]() ,得椭圆标准方程;
,得椭圆标准方程;
(2)设直线![]() 方程为
方程为![]() ,可求得
,可求得![]() 的坐标,由
的坐标,由![]() 共线求得
共线求得![]() 点坐标,这样可求得
点坐标,这样可求得![]() ,令
,令![]() 换元后用基本不等式求得最大值.
换元后用基本不等式求得最大值.
(1) 由题意得: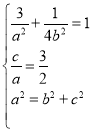 得a2=4,b2=1,
得a2=4,b2=1,
故椭圆C的标准方程为:![]() +y2=1.
+y2=1.
(2) 由题意设lAP:y=k(x+2),-![]() <k<0,所以C(0,2k),
<k<0,所以C(0,2k),
由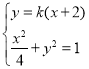 消y得(1+4k2)x2+16k2x+16k2-4=0,所以xAxP=
消y得(1+4k2)x2+16k2x+16k2-4=0,所以xAxP=![]() ,
,
由xA=-2得xP=![]() ,故yP=k(xP+2)=
,故yP=k(xP+2)=![]() ,
,
所以P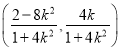 ,
,
设D(x0,0),因B(0,1),P,B,D三点共,所以kBD=kPB,故![]() =
=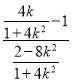 ,
,
解得x0=![]() ,得D
,得D![]() ,
,
所以S△PCD=SPAD-S△CAD=![]() ×AD×|yP-yC|
×AD×|yP-yC|
=![]() =
=![]() ,
,
因为-![]() <k<0,所以S△PCD=
<k<0,所以S△PCD=![]() =-2+2×
=-2+2×![]() ,
,
令t=1-2k,1<t<2,所以2k=1-t,
所以g(t)=-2+![]() =-2+
=-2+![]()
=-2+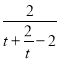 ≤-2+
≤-2+![]() =
=![]() -1,
-1,
当且仅当t=![]() 时取等号,此时k=
时取等号,此时k=![]() ,所以△PCD面积的最大值为
,所以△PCD面积的最大值为![]() -1.
-1.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点
为参数),以直角坐标系的原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,求三条曲线
,求三条曲线![]() ,
,![]() ,
,![]() 所围成图形的面积.
所围成图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知矩形![]() 所在平面与半圆弧
所在平面与半圆弧![]() 所在平面垂直,
所在平面垂直,![]() 是半圆弧
是半圆弧![]() 上异于
上异于![]() ,
,![]() 的点.
的点.
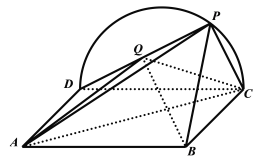
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,当三棱锥
,当三棱锥![]() 的体积最大且二面角
的体积最大且二面角![]() 的平面角的大小为
的平面角的大小为![]() 时,试确定
时,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.

(1)求A;
(2)若AD为BC边上的中线,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,M是椭圆C的上顶点,
,M是椭圆C的上顶点,![]() ,F2是椭圆C的焦点,
,F2是椭圆C的焦点,![]() 的周长是6.
的周长是6.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过动点P(1,t)作直线交椭圆C于A,B两点,且|PA|=|PB|,过P作直线l,使l与直线AB垂直,证明:直线l恒过定点,并求此定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:y2=4x的焦点为F,过F的直线l与C交于A,B两点,点M的坐标为(﹣1,0).
(1)当l与x轴垂直时,求△ABM的外接圆方程;
(2)记△AMF的面积为S1,△BMF的面积为S2,当S1=4S2时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点Q是圆![]() 上的动点,点
上的动点,点![]() ,若线段QN的垂直平分线MQ于点P.
,若线段QN的垂直平分线MQ于点P.
(I)求动点P的轨迹E的方程
(II)若A是轨迹E的左顶点,过点D(-3,8)的直线l与轨迹E交于B,C两点,求证:直线AB、AC的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某公司生产线生产的某种产品中抽取![]() 件,测量这些产品的一项质量指标,由检测结果得如图所示的频率分布直方图:
件,测量这些产品的一项质量指标,由检测结果得如图所示的频率分布直方图:
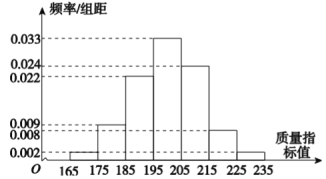
(Ⅰ)求这![]() 件产品质量指标的样本平均数
件产品质量指标的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)由直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ii)已知每件该产品的生产成本为![]() 元,每件合格品(质量指标值
元,每件合格品(质量指标值![]() )的定价为
)的定价为![]() 元;若为次品(质量指标值
元;若为次品(质量指标值![]() ),除了全额退款外且每件次品还须赔付客户
),除了全额退款外且每件次品还须赔付客户![]() 元。若该公司卖出
元。若该公司卖出![]() 件这种产品,记
件这种产品,记![]() 表示这件产品的利润,求
表示这件产品的利润,求![]() .
.
附:![]() .若
.若![]() ,则
,则![]()
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com