
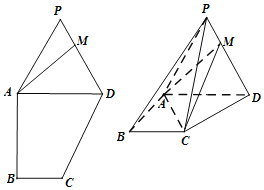
【题目】如图,在多边形PABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,M是线段PD上的一点,且
,M是线段PD上的一点,且![]() ,若将
,若将![]() 沿AD折起,得到几何体
沿AD折起,得到几何体![]() .
.
![]() 证明:
证明:![]() 平面AMC
平面AMC
![]() 若
若![]() ,且平面
,且平面![]() 平面ABCD,求三棱锥
平面ABCD,求三棱锥![]() 的体积.
的体积.
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源: 题型:
【题目】经统计分析,我市城区某拥挤路段的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当该路段的车流密度达到180辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为40千米/小时;当![]() 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当车流密度x为多大时,该拥挤路段车流量(单位时间内通过该路段某观测点的车辆数,单位:辆/小时)![]() 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的各项均为正数,2a2﹣5a1=3,a3a7=9a42;
(1)求数列{an}的通项公式;
(2)设bn=anlog3an,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年8月31日,十三届全国人大常委会第五次会议表决通过了关于修改个人所得税法的决定,这是我国个人所得税法自1980年出台以来第七次大修![]() 为了让纳税人尽早享受减税红利,在过渡期对纳税个人按照下表计算个人所得税,值得注意的是起征点变为5000元,即如表中“全月应纳税所得额”是纳税者的月薪金收入减去5000元后的余额.
为了让纳税人尽早享受减税红利,在过渡期对纳税个人按照下表计算个人所得税,值得注意的是起征点变为5000元,即如表中“全月应纳税所得额”是纳税者的月薪金收入减去5000元后的余额.
级数 | 全月应纳税所得额 | 税率 |
1 | 不超过3000元的部分 |
|
2 | 超过3000元至12000元的部分 |
|
3 | 超过12000元至25000元的部分 |
|
|
|
|
某企业员工今年10月份的月工资为15000元,则应缴纳的个人所得税为______元![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是城市慢行系统的一种创新模式,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20 000元,每生产一辆新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数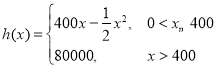 其中x是新样式单车的月产量(单位:辆),利润=总收益-总成本.
其中x是新样式单车的月产量(单位:辆),利润=总收益-总成本.
(1)试将自行车厂的利润y元表示为月产量x的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,且曲线
轴的正半轴为极轴建立极坐标系,且曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 上的定点
上的定点![]() 在曲线
在曲线![]() 外且其到
外且其到![]() 上的点的最短距离为
上的点的最短距离为![]() ,试求点
,试求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 且
且![]() .
.
(1)若函数![]() 在
在![]() 上恒有意义,求
上恒有意义,求![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 上为增函数,且最大值为
上为增函数,且最大值为![]() ?若存在求出
?若存在求出![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com