
【题目】某港口的水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下面是每天时间与水深的关系表:
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 10 | 13 | 9.9 | 7 | 10 | 13 | 10.1 | 7 | 10 |
经过长期观测,y=f(t)可近似的看成是函数y=Asinωt+b
(1)根据以上数据,求出y=f(t)的解析式;
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
【答案】解:(1)由表中数据可以看到:水深最大值为13,最小值为7,
∴b=![]() =10,A=
=10,A=![]()
且相隔9小时达到一次最大值说明周期为12,
因此T=![]() =12,
=12,![]() ,
,
故![]() (0≤t≤24)
(0≤t≤24)
(2)要想船舶安全,必须深度f(t)≥11.5,即![]()
∴![]() ,
,![]()
解得:12k+1≤t≤5+12k k∈Z
又0≤t≤24
当k=0时,1≤t≤5;
当k=1时,13≤t≤17;
故船舶安全进港的时间段为(1:00﹣5:00),(13:00﹣17:00).
【解析】(1)由表中数据可以看到:水深最大值为13,最小值为7,求出b和A;再借助于相隔9小时达到一次最大值说明周期为12求出ω即可求出y=f(t)的解析式;
(2)把船舶安全转化为深度f(t)≥11.5,即![]() ;再解关于t的三角不等式即可求出船舶在一天中的哪几段时间可以安全的进出该港.
;再解关于t的三角不等式即可求出船舶在一天中的哪几段时间可以安全的进出该港.


科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论: ①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为(注:把你认为正确的结论的序号都填上).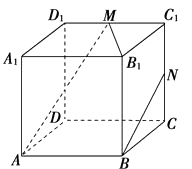
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述: ①函数 ![]() 是奇函数;
是奇函数;
②函数 ![]() 的一条对称轴方程为
的一条对称轴方程为 ![]() ;
;
③函数 ![]() ,
, ![]() ,则f(x)的值域为
,则f(x)的值域为 ![]() ;
;
④函数 ![]() 有最小值,无最大值.
有最小值,无最大值.
所有正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题
(1)已知α为第二象限角,且 sinα= ![]() ,求
,求 ![]() 的值.
的值.
(2)已知α∈(0, ![]() ),β∈(0,π),且tan(α﹣β)=
),β∈(0,π),且tan(α﹣β)= ![]() ,tanβ=﹣
,tanβ=﹣ ![]() ,求tan(2α﹣β)的值及角2α﹣β.
,求tan(2α﹣β)的值及角2α﹣β.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=6cos2 ![]() +
+ ![]() sinωx﹣3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
sinωx﹣3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形. 
(1)求ω的值及函数f(x)的值域;
(2)若f(x0)= ![]() ,且x0∈(﹣
,且x0∈(﹣ ![]() ,
, ![]() ),求f(x0+1)的值.
),求f(x0+1)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,a14+a15+a16=﹣54,a9=﹣36,Sn为其前n项和.
(1)求Sn的最小值,并求出相应的n值;
(2)求Tn=|a1|+|a2|+…+|an|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有教职员工150人,其中高级职称15人,中级职称45人,一般职员90人,现在用分层抽样抽取30人,则样本中各职称人数分别为( )
A.5,10,15
B.3,9,18
C.3,10,17
D.5,9,16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x2+ex﹣ ![]() (x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
(x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
A.(﹣ ![]() )
)
B.( ![]() )
)
C.( ![]() )
)
D.( ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com