
分析 (1)由周期求出ω,由图象的对称轴求出φ的值,可得函数的解析式.
(2)利用同角三角的基本关系求得sin(α-$\frac{π}{6}$)的值,再利用两角和差的正弦公式求得$sinα=sin[{(α-\frac{π}{6})+\frac{π}{6}}]$ 的值.
解答 解:(1)因f(x)的图象上相邻两个最高点的距离为π,
所以f(x)的最小正周期T=$\frac{2π}{ω}$=π,从而$ω=\frac{2π}{T}=2$,
又因为f(x)的图象关于直线$x=\frac{π}{3}$对称,所以$2×\frac{π}{3}+φ=kπ+\frac{π}{2}(k∈Z)$.
因为$-\frac{π}{2}≤φ<\frac{π}{2}$,所以k=0,得$φ=-\frac{π}{6}$,∴$f(x)=\sqrt{3}sin(2x-\frac{π}{6})$.
(2)由(1)得$f(\frac{α}{2})=\sqrt{3}sin(2•\frac{α}{2}-\frac{π}{6})=\frac{{4\sqrt{3}}}{5}$,所以$sin(α-\frac{π}{6})=\frac{4}{5}$,
由$\frac{π}{6}<α<\frac{2π}{3}$,得$0<α-\frac{π}{6}<\frac{π}{2}$,∴$cos(α-\frac{π}{6})=\sqrt{1-{{sin}^2}(α-\frac{π}{6})}=\frac{3}{5}$,
因此$sinα=sin[{(α-\frac{π}{6})+\frac{π}{6}}]$=$sin(α-\frac{π}{6})cos\frac{π}{6}+cos(α-\frac{π}{6})sin\frac{π}{6}$=$\frac{4}{5}×\frac{{\sqrt{3}}}{2}+\frac{3}{5}×\frac{1}{2}=\frac{{4\sqrt{3}+3}}{10}$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由图象的对称轴求出φ的值.还考查了,同角三角的基本关系,两角和差的正弦公式属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$$\overrightarrow{EF}$+$\frac{1}{2}$$\overrightarrow{EG}$+$\frac{1}{2}$$\overrightarrow{EH}$ | B. | $\frac{1}{5}$$\overrightarrow{EF}$+$\frac{1}{5}$$\overrightarrow{EG}$+$\frac{1}{5}$$\overrightarrow{EH}$ | C. | $\frac{1}{4}$$\overrightarrow{EF}$+$\frac{1}{4}$$\overrightarrow{EG}$+$\frac{1}{4}$$\overrightarrow{EH}$ | D. | $\frac{1}{3}$$\overrightarrow{EF}$+$\frac{1}{3}$$\overrightarrow{EG}$+$\frac{1}{3}$$\overrightarrow{EH}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0或-1 | B. | 0或-2 | C. | 0或1 | D. | 0或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
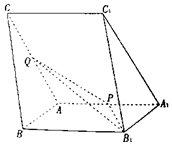 如图,三棱柱ABC-A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1,AC的中点.
如图,三棱柱ABC-A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1,AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com