
分析 化简$\frac{{n}^{3}-1}{3{n}^{2}+n}$-$\frac{{n}^{2}+1}{3n+4}$=$\frac{3{n}^{3}-3{n}^{2}-4n-4}{9{n}^{3}+15{n}^{2}+4n}$,从而求极限即可.
解答 解:$\frac{{n}^{3}-1}{3{n}^{2}+n}$-$\frac{{n}^{2}+1}{3n+4}$
=$\frac{({n}^{3}-1)(3n+4)-(3{n}^{2}+n)({n}^{2}+1)}{9{n}^{3}+15{n}^{2}+4n}$
=$\frac{3{n}^{3}-3{n}^{2}-4n-4}{9{n}^{3}+15{n}^{2}+4n}$,
故$\underset{lim}{n→∞}$($\frac{{n}^{3}-1}{3{n}^{2}+n}$-$\frac{{n}^{2}+1}{3n+4}$)
=$\underset{lim}{n→∞}$$\frac{3{n}^{3}-3{n}^{2}-4n-4}{9{n}^{3}+15{n}^{2}+4n}$
=$\underset{lim}{n→∞}$$\frac{3-\frac{3}{n}-\frac{4}{{n}^{2}}-\frac{4}{{n}^{3}}}{9+\frac{15}{n}+\frac{4}{{n}^{2}}}$
=$\frac{1}{3}$;
故答案为:$\frac{1}{3}$.
点评 本题考查了分式的化简与极限的求法应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
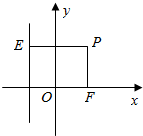 如图,点O是坐标原点,点F(p,0),其中p>0,点E在直线l:x=-p上,点F到直线x+y=0的距离等于$\sqrt{2}$,动点p满足|$\overrightarrow{PE}$|=|$\overrightarrow{FP}$|,$\overrightarrow{EP}$=λ$\overrightarrow{OF}$(λ∈R,且λ≠0).
如图,点O是坐标原点,点F(p,0),其中p>0,点E在直线l:x=-p上,点F到直线x+y=0的距离等于$\sqrt{2}$,动点p满足|$\overrightarrow{PE}$|=|$\overrightarrow{FP}$|,$\overrightarrow{EP}$=λ$\overrightarrow{OF}$(λ∈R,且λ≠0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$x2-18x+20 | B. | -$\frac{1}{2}$x2+18x-20 | C. | $\frac{1}{2}$x2+2x | D. | $\frac{1}{2}$x2-18x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com