
分析 (I)分类讨论,即可解不等式;
(II)利用绝对值不等式,即可证明.
解答 (Ⅰ)解:当a=1时,不等式f(x)≥2,即|x-1|+|2x-1|≥2.
x<$\frac{1}{2}$时,不等式可化为1-x+1-2x≥2,解得x≤0,∴x≤0;
$\frac{1}{2}≤x≤1$时,不等式可化为1-x+2x-1≥2,解得x≥2,∴x无解;
x>1时,不等式可化为x-1+2x-1≥2,解得x≥$\frac{4}{3}$,∴x≥$\frac{4}{3}$;
综上所述,不等式的解集为(-∞,0]∪[$\frac{4}{3}$,+∞);
(Ⅱ)证明:f(x)=|x-a|+|2x-1|≥|a-x|+|x-$\frac{1}{2}$|≥|a-$\frac{1}{2}$|.
点评 本题考查不等式的解法与证明,考查分类讨论的数学思想,考查绝对值不等式的运用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
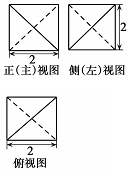
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com