
分析 (1)根据条件Sn≥S5可知{an}前5项为负数或0,第6项后为整数,列出不等式得出d,即可得出通项公式;
(2)n为偶数时,${b_n}+{b_{n+1}}={(-2)^n}={2^n}$.利用此性质再根据n的奇偶性计算Tn;
(3)令cn+1-cn>0,分离参数得出λ关于n的不等式,根据数列的单调性得出λ的最值即可得出λ的取值范围.
解答 解:(1)设{an}的公差为d,由题意得$\left\{\begin{array}{l}{a_5}≤0\\{a_6}≥0\end{array}\right.$,∴$\frac{9}{5}≤d≤\frac{9}{4}$,
∵a2∈Z,即-9+d是整数,∴d=2﹒∴an=-9+2(n-1)=2n-11.
(2)当n为偶数时,${b_n}+{b_{n+1}}={(-2)^n}={2^n}$.
①当n为奇数时(n≥3),Tn=b1+(b2+b3)+(b4+b5)+…+(bn-1+bn)=${b_1}+{2^2}+{2^4}+…+{2^{n-1}}$=$\frac{4}{3}+\frac{{4(1-{4^{\frac{n-1}{2}}})}}{1-4}=\frac{{{2^{n+1}}}}{3}$.
当n=1时也符合上式.
②当n为偶数时,${T_n}={T_{n-1}}+{b_n}=\frac{2^n}{3}+{a_{n-1}}=\frac{2^n}{3}+2n-13$﹒
∴${T_n}=\left\{\begin{array}{l}\frac{{{2^{n+1}}}}{3},\;\;\;\;\;\;\;\;\;\;\;n为奇数\\ \frac{2^n}{3}+2n-13,\;n为偶数.\end{array}\right.$﹒
(3)${c_n}={4^n}+λ{(-1)^n}{(\frac{1}{4})^{n-3}}$,
假设{cn}是单调递增数列,
则${c_{n+1}}-{c_n}=3•{4^n}-80λ{(-\frac{1}{4})^n}>0$对任意n∈N*都成立,
当n为奇数时,$λ>-\frac{3}{80}•{4^{2n}}$,
令f(n)=-$\frac{3}{80}$•42n,则f(n)单调递减,∴f(n)≤f(1)=-$\frac{3}{5}$,
∴$λ>-\frac{3}{5}$﹒
当n为偶数时,$λ<\frac{3}{80}•{4^{2n}}$,
令g(n)=$\frac{3}{80}$•42n,则g(n)单调递增,∴g(n)≥g(2)=$\frac{48}{5}$,
∴λ<$\frac{48}{5}$.
综上:$λ∈(-\frac{3}{5},\;\frac{48}{5})$.
点评 本题考查了等差数列的性质,数列的求和,数列单调性的判断,属于中档题.


 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
 定义n!=1×2×3×…×n,例如1!=1,2!=1×2=2,执行右边的程序框图,若输入?=0.01,则输出的e精确到e的近似值为( )
定义n!=1×2×3×…×n,例如1!=1,2!=1×2=2,执行右边的程序框图,若输入?=0.01,则输出的e精确到e的近似值为( )| A. | 2.69 | B. | 2.70 | C. | 2.71 | D. | 2.72 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
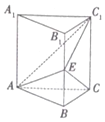 如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.
如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
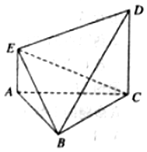 如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.
如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x≤5} | B. | {x|2<x≤3} | C. | {x|1≤x<2或3≤x≤5}} | D. | {x|1≤x≤5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com