
【题目】如图,四棱锥![]() 中,平面
中,平面![]() 底面
底面![]() ,
,![]() 是等边三角形,底面
是等边三角形,底面![]() 是菱形,且
是菱形,且![]() ,
,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为菱形
为菱形![]() 的中心,下列结论正确的有( )
的中心,下列结论正确的有( )
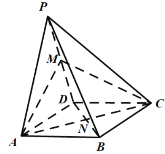
A.直线![]() 与平面
与平面![]() 平行B.直线
平行B.直线![]() 与直线
与直线![]() 垂直
垂直
C.线段![]() 与线段
与线段![]() 长度相等D.
长度相等D.![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,使用手机上网成为了人们日常生活的一部分,很多消费者对手机流量的需求越来越大.某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了人口规模相当的![]() 个城市采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价:
个城市采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价: ![]() (单位:元/月)和购买总人数
(单位:元/月)和购买总人数![]() (单位:万人)的关系如表:
(单位:万人)的关系如表:
定价x(元/月) | 20 | 30 | 50 | 60 |
年轻人(40岁以下) | 10 | 15 | 7 | 8 |
中老年人(40岁以及40岁以上) | 20 | 15 | 3 | 2 |
购买总人数y(万人) | 30 | 30 | 10 | 10 |
(Ⅰ)根据表中的数据,请用线性回归模型拟合![]() 与
与![]() 的关系,求出
的关系,求出![]() 关于
关于![]() 的回归方程;并估计
的回归方程;并估计![]() 元/月的流量包将有多少人购买?
元/月的流量包将有多少人购买?
(Ⅱ)若把![]() 元/月以下(不包括
元/月以下(不包括![]() 元)的流量包称为低价流量包,
元)的流量包称为低价流量包,![]() 元以上(包括
元以上(包括![]() 元)的流量包称为高价流量包,试运用独立性检验知识,填写下面列联,并通过计算说明是否能在犯错误的概率不超过
元)的流量包称为高价流量包,试运用独立性检验知识,填写下面列联,并通过计算说明是否能在犯错误的概率不超过![]() 的前提下,认为购买人的年龄大小与流量包价格高低有关?
的前提下,认为购买人的年龄大小与流量包价格高低有关?
定价x(元/月) | 小于50元 | 大于或等于50元 | 总计 |
年轻人(40岁以下) | |||
中老年人(40岁以及40岁以上) | |||
总计 |
参考公式:其中![]()
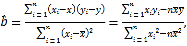
![]()
![]() 其中
其中![]()
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网购人数的日益增多,网上的支付方式也呈现一种多样化的状态,越来越多的便捷移动支付方式受到了人们的青睐,更被网友们评为“新四大发明”之一.随着人们消费观念的进步,许多人喜欢用信用卡购物,考虑到这一点,一种“网上的信用卡”横空出世——蚂蚁花呗.这是一款支付宝和蚂蚁金融合作开发的新支付方式,简单便捷,同时也满足了部分网上消费群体在支付宝余额不足时的“赊购”消费需求.为了调查使用蚂蚁花呗“赊购”消费与消费者年龄段的关系,某网站对其注册用户开展抽样调查,在每个年龄段的注册用户中各随机抽取100人,得到各年龄段使用蚂蚁花呗“赊购”的人数百分比如图所示.
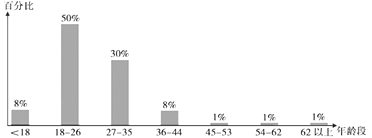
(1)由大数据可知,在18到44岁之间使用花呗“赊购”的人数百分比y与年龄x成线性相关关系,利用统计图表中的数据,以各年龄段的区间中点代表该年龄段的年龄,求所调查群体各年龄段“赊购”人数百分比y与年龄x的线性回归方程(回归直线方程的斜率和截距保留两位有效数字);
(2)该网站年龄为20岁的注册用户共有2000人,试估算该网站20岁的注册用户中使用花呗“赊购”的人数;
(3)已知该网店中年龄段在18-26岁和27-35岁的注册用户人数相同,现从18到35岁之间使用花呗“赊购”的人群中按分层抽样的方法随机抽取8人,再从这8人中简单随机抽取2人调查他们每个月使用花呗消费的额度,求抽取的两人年龄都在18到26岁的概率.
参考答案: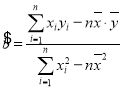 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着移动互联网的发展,与餐饮美食相关的手机APP软件层出不穷.现从某市使用A和B两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下.


![]()
![]()
(1)已知抽取的100个使用A款订餐软件的商家中,甲商家的“平均送达时间”为18分钟。现从使用A款订餐软件的商家中“平均送达时间”不超过20分钟的商家中随机抽取3个商家进行市场调研,求甲商家被抽到的概率;
(2)试估计该市使用A款订餐软件的商家的“平均送达时间”的众数及平均数;
(3)如果以“平均送达时间”的平均数作为决策依据,从A和B两款订餐软件中选择一款订餐,你会选择哪款?
查看答案和解析>>
科目:高中数学 来源: 题型:
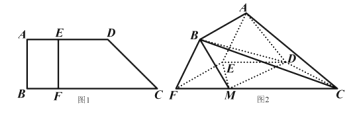
【题目】如图1,直角梯形![]() 中,
中,![]() ,
,![]() ,E、F分别是
,E、F分别是![]() 和
和![]() 上的点,且
上的点,且![]() ,
,![]() ,
,![]() ,沿
,沿![]() 将四边形
将四边形![]() 折起,如图2,使
折起,如图2,使![]() 与
与![]() 所成的角为60°.
所成的角为60°.
(1)求证:![]() 平面
平面![]() ;
;
(2)M为![]() 上的点,
上的点,![]() ,若二面角
,若二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为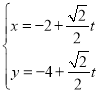 (t为参数),以坐标原点O为极点,以x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点O为极点,以x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)写出直线![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)已知定点![]() ,直线
,直线![]() 与曲线C分别交于P、Q两点,求
与曲线C分别交于P、Q两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,已知曲线C1:x2+y2=1,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() :ρ(2cosθ-sinθ)=6.
:ρ(2cosθ-sinθ)=6.
(Ⅰ)将曲线C1上的所有点的横坐标,纵坐标分别伸长为原来的![]() 、2倍后得到曲线C2,试写出直线
、2倍后得到曲线C2,试写出直线![]() 的直角坐标方程和曲线C2的参数方程.
的直角坐标方程和曲线C2的参数方程.
(Ⅱ)在曲线C2上求一点P,使点P到直线l的距离最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为折痕把
为折痕把![]() 折起,当几何体
折起,当几何体![]() 的的体积最大时,则下列命题中正确的个数是( )
的的体积最大时,则下列命题中正确的个数是( )

①![]()
②![]() ∥平面
∥平面![]()
③![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角
所成的角
④![]() 与
与![]() 所成的角等于
所成的角等于![]() 与
与![]() 所成的角
所成的角
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com