
【题目】(本题满分14分)
已知椭圆C:![]() 过点
过点![]() ,且长轴长等于4.
,且长轴长等于4.
(Ⅰ)求椭圆C的方程;
(Ⅱ)![]() 是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若
是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ,(2)
,(2)![]()
【解析】
解:(Ⅰ)由题意椭圆的长轴2![]() =4,得a=2, -------------------------1分
=4,得a=2, -------------------------1分
![]() 点
点![]() 在椭圆上,
在椭圆上,![]() ----------3分
----------3分
∴椭圆的方程为![]() -------------------------------5分
-------------------------------5分
(Ⅱ)由直线l与圆O相切得![]() ---------------6分
---------------6分
设![]() ,
,
由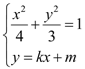 消去
消去![]() ,整理得
,整理得![]() ------7分
------7分
由题可知圆O在椭圆内,所以直线必与椭圆相交![]() -------------------------8分
-------------------------8分
![]()
![]() --------------------------------------9分
--------------------------------------9分
![]() =
=![]()
=![]() =
=![]() -------------------10分
-------------------10分
![]() ----------------------11分
----------------------11分
![]()
![]() --------------------12分
--------------------12分
![]() -------14分
-------14分


科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,
,![]() (n∈N*).
(n∈N*).
(1)证明数列![]() 是等比数列,求出数列
是等比数列,求出数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ;
;
(3)数列![]() 中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,近日我渔船编队在岛![]() 周围海域作业,在岛
周围海域作业,在岛![]() 的南偏西20°方向有一个海面观测站
的南偏西20°方向有一个海面观测站![]() ,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与
,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与![]() 相距31海里的
相距31海里的![]() 处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛
处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛![]() 直线航行以保护我渔船编队,30分钟后到达
直线航行以保护我渔船编队,30分钟后到达![]() 处,此时观测站测得
处,此时观测站测得![]() 间的距离为21海里.
间的距离为21海里.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试问海警船再向前航行多少分钟方可到岛![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市在进行规划时,准备设计一个圆形的开放式公园.为达到社会和经济效益双丰收.园林公司进行如下设计,安排圆内接四边形![]() 作为绿化区域,其余作为市民活动区域.其中
作为绿化区域,其余作为市民活动区域.其中![]() 区域种植花木后出售,
区域种植花木后出售,![]() 区域种植草皮后出售,已知草皮每平方米售价为
区域种植草皮后出售,已知草皮每平方米售价为![]() 元,花木每平方米的售价是草皮每平方米售价的三倍. 若
元,花木每平方米的售价是草皮每平方米售价的三倍. 若![]() km ,
km ,![]() km
km
(1)若![]() km ,求绿化区域的面积;
km ,求绿化区域的面积;
(2)设![]() ,当
,当![]() 取何值时,园林公司的总销售金额最大.
取何值时,园林公司的总销售金额最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地棚户区改造建筑平面示意图如图所示,经规划调研确定,棚改规划建筑用地区域近似为圆面,该圆面的内接四边形![]() 是原棚户区建筑用地,测量可知边界
是原棚户区建筑用地,测量可知边界![]() 万米,
万米,![]() 万米,
万米,![]() 万米.
万米.
(1)请计算原棚户区建筑用地![]() 的面积及
的面积及![]() 的长;
的长;
(2)因地理条件的限制,边界![]() 不能更改,而边界
不能更改,而边界![]() 可以调整,为了提高棚户区建筑用地的利用率,请在圆弧
可以调整,为了提高棚户区建筑用地的利用率,请在圆弧![]() 上设计一点
上设计一点![]() ,使得棚户区改造后的新建筑用地
,使得棚户区改造后的新建筑用地![]() 的面积最大,并求出最大值.
的面积最大,并求出最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,点
,点![]() 在椭圆上,有
在椭圆上,有![]() ,椭圆的离心率为
,椭圆的离心率为![]() ;
;
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,过点
,过点![]() 作直线
作直线![]() 与椭圆交于
与椭圆交于![]() 不同两点,线段
不同两点,线段![]() 的中垂线为
的中垂线为![]() ,线段
,线段![]() 的中点为
的中点为![]() 点,记
点,记![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列{an},记T={x|x=aj﹣ai,i<j},若数列{an}满足:“存在t∈T,使得只要am﹣ak=t(m,k∈N*,m>k),必有am+1﹣ak+1=t”,则称数列具有性质P(t).
(1)若数列{an}满足![]() ,判断数列{an}是否具有性质P(2)?是否具有性质P(4)?说明理由;
,判断数列{an}是否具有性质P(2)?是否具有性质P(4)?说明理由;
(2)求证:“T是有限集”是“数列{an}具有性质P(0)”的必要不充分条件;
(3)已知{bn}是各项均为正整数的数列,且{bn}既具有性质P(2),又具有性质P(5),求证:存在正整数N,使得aN,aN+1,aN+2,…,aN+K,…是等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com