
在数列{an}中,已知a1=2,a2=3,当n≥2时,an+1是an•an﹣1的个位数,则a2010=
4
解析试题分析:由题意得,a3=a1•a2=6,a4=8,a5=8,a6=4,a7=2,a8=8,a9=6,a10=8,到此为止,看出一个周期,a9=a3,a10=a4,周期为6,利用这个周期能求出a2010.
由题意得,a3=a1•a2=6,定义f(x)=x的个位数
则a4=f(a3•a2)=8,
依此类推,a5=8,a6=4,a7=2,a8=8,a9=6,a10=8,
到此为止,看出一个周期,a9=a3,a10=a4,周期为6,
因为前2项不符合周期,所以2010﹣2=2008,2008=6×334+4,
所以a2010=a6=4.
故答案为:4.
考点:数列递推式
点评:本题考查数列的性质和应用,解题时要注意数列递推式的合理运用和周期性的灵活运用.


科目:高中数学 来源: 题型:填空题
数列 满足
满足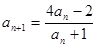 (
(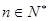 ).
).
①存在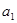 可以生成的数列
可以生成的数列 是常数数列;
是常数数列;
②“数列 中存在某一项
中存在某一项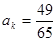 ”是“数列
”是“数列 为有穷数列”的充要条件;
为有穷数列”的充要条件;
③若 为单调递增数列,则
为单调递增数列,则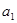 的取值范围是
的取值范围是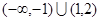 ;
;
④只要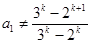 ,其中
,其中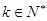 ,则
,则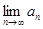 一定存在;
一定存在;
其中正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知数列{an}是首项a1=4,公比q≠1的等比数列,Sn是其前n项和,且4a1,a5,-2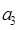 成等差数列.
成等差数列.
(1)求公比q的值;
(2)求Tn=a2+a4+a6+…+a2n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com