
【题目】如图1在正方形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,把
的中点,把![]() 沿
沿![]() 折叠,使
折叠,使![]() 为等边三角形,得到如图2所示的几何体.
为等边三角形,得到如图2所示的几何体.
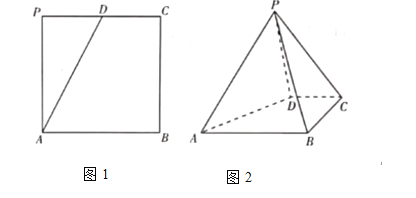
(Ⅰ)证明:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
(I)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,证得
,证得![]() 和
和![]() ,证得
,证得![]() 平面
平面![]() ,进而得到
,进而得到![]() .
.
(Ⅱ)由(Ⅰ)证得![]() ,分别以
,分别以![]() ,
,![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴的正方向,过点
轴的正方向,过点![]() 垂直于平面
垂直于平面![]() 的直线为
的直线为![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() ,分别求得平面
,分别求得平面![]() 和平面
和平面![]() 的一个法向量,结合向量的夹角公式,即可求解.
的一个法向量,结合向量的夹角公式,即可求解.
(I)依题意,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
则![]() ,
,![]() ,所以四边形
,所以四边形![]() 为矩形,所以
为矩形,所以![]() ,
,
因为![]() 为等边三角形,所以
为等边三角形,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
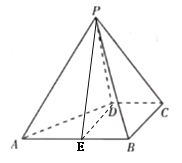
(Ⅱ)由(Ⅰ)知,![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
点![]() 到平面
到平面![]() 的距离即点
的距离即点![]() 到
到![]() 的距离,
的距离,
因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
在![]() 中,可得
中,可得![]() 到
到![]() 的距离为
的距离为![]() ,
,
分别以![]() ,
,![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴的正方向,过点
轴的正方向,过点![]() 垂直于平面
垂直于平面![]() 的直线为
的直线为![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以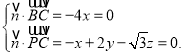 取
取![]() ,则
,则![]() ,
,
而平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则 ,
,
由图可知,二面角![]() 为钝角,所以所求的余弦值为
为钝角,所以所求的余弦值为![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】阿波罗尼斯(约公元前![]() 年)证明过这样一个命题:平面内到两定点距离之比为常数
年)证明过这样一个命题:平面内到两定点距离之比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点![]() 、
、![]() 间的距离为
间的距离为![]() ,动点
,动点![]() 满足
满足![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位在2019年重阳节组织50名退休职工(男、女各25名)旅游,退休职工可以选择到甲、乙两个景点其中一个去旅游.他们最终选择的景点的结果如下表:
男性 | 女性 | |
甲景点 | 20 | 10 |
乙景点 | 5 | 15 |
(1)据此资料分析,是否有![]() 的把握认为选择哪个景点与性别有关?
的把握认为选择哪个景点与性别有关?
(2)按照游览不同景点用分层抽样的方法,在女职工中选取5人,再从这5人中随机抽取2人进行采访,求这2人游览的景点不同的概率.
附: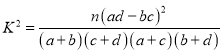 ,
,![]() .
.
P( | 0.010 | 0.005 | 0.001 |
k | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知多面体ABCDEF中,四边形ABFE为正方形,![]() ,
,![]() ,G为AB的中点,
,G为AB的中点,![]() .
.
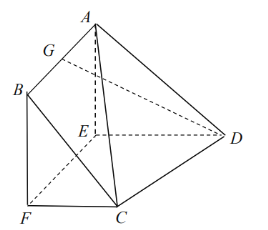
(1)求证:![]() 平面CDEF;
平面CDEF;
(2)求平面ACD与平面BCF所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与椭圆
与椭圆![]() 相交于点M(0,1),N(0,-1),且椭圆的离心率为
相交于点M(0,1),N(0,-1),且椭圆的离心率为![]() .
.
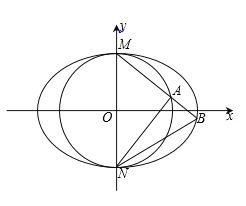
(1)求![]() 的值和椭圆C的方程;
的值和椭圆C的方程;
(2)过点M的直线![]() 交圆O和椭圆C分别于A,B两点.
交圆O和椭圆C分别于A,B两点.
①若![]() ,求直线
,求直线![]() 的方程;
的方程;
②设直线NA的斜率为![]() ,直线NB的斜率为
,直线NB的斜率为![]() ,问:
,问:![]() 是否为定值? 如果是,求出定值;如果不是,说明理由.
是否为定值? 如果是,求出定值;如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].从样本成绩不低于80分的学生中随机选取2人,记这2人成绩在90分以上(含90分)的人数为ξ,则ξ的数学期望为( )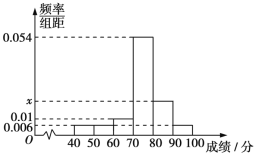
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com