练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若一个三角形的三个内角成等差数列，且其中一角为28°，则其中最大角的度数为________．

    92°
    分析：若三角形的三个内角成等差数列，则中间的内角为60°，由此能求出其中最大角的度数．
    解答：∵三角形的三个内角成等差数列，
    ∴中间的内角为60°，
    ∴其中最大角的度数为180°-60°-28°=92°．
    故答案为92°．
    点评：本题考查等差数列的性质和应用，解题时要注意三角形内角和公式的灵活运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2012•眉山一模）设函数f（x）对其定义域内的任意实数x1与x2都有f(
    x1+x2
    2
    )≥
    f(x1)+f(x2)
    2
    ，则称函数f（x）为上凸函数． 若函数f（x）为上凸函数，则对定义域内任意x1、x2、x3，…，xn都有f(
    x1+x2+…+xn
    n
    )≥
    f(x1)+f(x2)+…+f(xn)
    n
    （当x1=x2=x3=…=xn时等号成立），称此不等式为琴生不等式，现有下列命题：
    ①f（x）=lnx（x＞0）是上凸函数；
    ②二次函数f（x）=ax2+bx+c（a≠0）是上凸函数的充要条件是a＞0；
    ③f（x）是上凸函数，若A（x1，f（x1）），B（x2，f（x2））是f（x）图象上任意两点，点C在线段AB上，且
    AC
    =λ
    CB
    ，则f(
    x1+λx2
    1+λ
    )≥
    f(x1)+λf(x2)
    1+λ
    ；
    ④设A，B，C是一个三角形的三个内角，则sinA+sinB+sinC的最大值是
    3
    		3
    2
    ．
    其中，正确命题的序号是
    ①③④
    ①③④
    （写出所有你认为正确命题的序号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列命题：

    （1）若a=0,则任意向量b都有a·b=0；

    （2）若a≠0,则任意实数λ都有λ·a≠0；

    （3）若++=0，则A、B、C为一个三角形的三个顶点；

    （4）一个平面内任意两个向量可作为表示该平面所有向量的基底．

    其中正确的命题为_______________．（填命题序号）

    查看答案和解析>>

    科目：高中数学 来源：2012年四川省眉山市高考数学一模试卷（理科）（解析版） 题型：解答题

    设函数f（x）对其定义域内的任意实数，则称函数f（x）为上凸函数． 若函数f（x）为上凸函数，则对定义域内任意x1、x2、x3，…，xn都有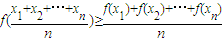（当x1=x2=x3=…=xn时等号成立），称此不等式为琴生不等式，现有下列命题：
    ①f（x）=lnx（x＞0）是上凸函数；
    ②二次函数f（x）=ax2+bx+c（a≠0）是上凸函数的充要条件是a＞0；
    ③f（x）是上凸函数，若A（x1，f（x1）），B（x2，f（x2））是f（x）图象上任意两点，点C在线段AB上，且；
    ④设A，B，C是一个三角形的三个内角，则sinA+sinB+sinC的最大值是．
    其中，正确命题的序号是    （写出所有你认为正确命题的序号）．

    查看答案和解析>>

    科目：高中数学 来源：四川省模拟题 题型：填空题

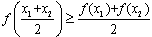    设函数f（x）对其定义域内的任意实数x1与x2都有，则称函数f（x）为上凸函数． 若函数f（x）为上凸函数，则对定义域内任意x1、x2、x3，…，xn都有（当x1=x2=x3=…=xn时等号成立），称此不等式为琴生不等式，现有下列命题：
    ①f（x）=lnx（x＞0）是上凸函数；
    ②二次函数f（x）=ax2+bx+c（a≠0）是上凸函数的充要条件是a＞0；
    ③f（x）是上凸函数，若A（x1，f（x1）），B（x2，f（x2））是f（x）图象上任意两点，点C在线段AB上，且，则；
    ④设A，B，C是一个三角形的三个内角，则sinA+sinB+sinC的最大值是．
    其中，正确命题的序号是（     ）（写出所有你认为正确命题的序号）．

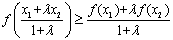    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题：①若，则；

    ②与非零向量共线的单位向量是；

    ③若，则A,B,C是一个三角形的三个顶点;

    ④若，则至少有一个是；

    ⑤已知A,B,C是不共线的三点，G是内一点，若，则G是的重心。其中真命题的个数是（   ）

    A. 个      B.个      C. 个     D.个

    查看答案和解析>>

    同步练习册答案