解:(1)记第i名工人选择甲,乙,丙型车床分别为事件A
i,B
i,C
i,i=1,2,3.
由题意知A
1,A
2,A
3相互独立,
B
1,B
2,B
3相互独立,
C
1,C
2,C
3相互独立
A
i,B
j,B
k(i,j,k=1,2,3,且i,j,k互不相同)相互独立,
且
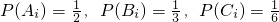
,
他们选择的车床类型互不相同的概率为
P=3!P(A
1B
2C
3)
=6×
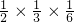
=

.
(2)解法一:设3名工人中选择乙型车床的人数为η,
则η~
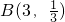
,
且ξ=3-η.
所以P(ξ=k)=P(η=3-k)=
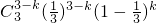
.
故ξ的分布列为
所以,ξ的数学期望为Eξ=3-Eη=3-3×

=2.
解法二:设第i名工人选择甲或丙型车床记为事件D
i(i=1,2,3),
则D
1,D
2,D
3相互独立,
且
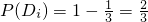
.
所以ξ~B(3,

),
即
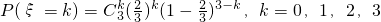
.
故ξ的分布列为
所以,ξ的数学期望为Eξ=3×

=2.
分析:(1)记第i名工人选择甲,乙,丙型车床分别为事件A
i,B
i,C
i,i=1,2,3.由题意知A
1,A
2,A
3相互独立,B
1,B
2,B
3相互独立,C
1,C
2,C
3相互独立A
i,B
j,B
k(i,j,k=1,2,3,且i,j,k互不相同)相互独立,
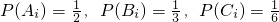
,由此能求出他们选择的车床类型互不相同的概率为P=3!P(A
1B
2C
3).
(2)法一:设3名工人中选择乙型车床的人数为η,则η~
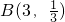
,且ξ=3-η.由此能求出ξ的分布列和ξ的数学期望.法二:设第i名工人选择甲或丙型车床记为事件D
i(i=1,2,3),则D
1,D
2,D
3相互独立,且
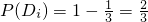
.所以ξ~B(3,

),由此能求出ξ的分布列和ξ的数学期望.
点评:本题考查离散型随机变量的分布列和数学期望,解题时要认真审题,仔细解答,注意二项分布的性质的灵活运用.

 ,
, ,
, ,现在有三名工人各自独立选一台车床操作.
,现在有三名工人各自独立选一台车床操作.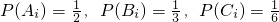 ,
,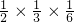 =
= .
.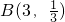 ,
,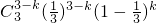 .
.



 =2.
=2.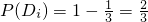 .
. ),
),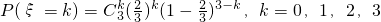 .
.



 =2.
=2.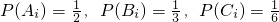 ,由此能求出他们选择的车床类型互不相同的概率为P=3!P(A1B2C3).
,由此能求出他们选择的车床类型互不相同的概率为P=3!P(A1B2C3).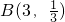 ,且ξ=3-η.由此能求出ξ的分布列和ξ的数学期望.法二:设第i名工人选择甲或丙型车床记为事件Di(i=1,2,3),则D1,D2,D3相互独立,且
,且ξ=3-η.由此能求出ξ的分布列和ξ的数学期望.法二:设第i名工人选择甲或丙型车床记为事件Di(i=1,2,3),则D1,D2,D3相互独立,且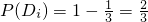 .所以ξ~B(3,
.所以ξ~B(3, ),由此能求出ξ的分布列和ξ的数学期望.
),由此能求出ξ的分布列和ξ的数学期望.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案 ,
, ,
, ,现在有三名工人各自独立选一台车床操作.
,现在有三名工人各自独立选一台车床操作.