
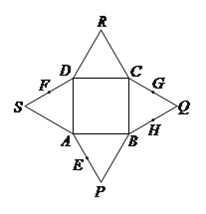
【题目】如图,已知四边形![]() 是正方形,
是正方形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 都是等边三角形,
都是等边三角形, ![]() 、
、![]() 、
、![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 、
、![]() 、
、![]() 的中点,分别以
的中点,分别以![]() 、
、![]() 、
、![]() 、
、![]() 为折痕将四个等边三角形折起,使得
为折痕将四个等边三角形折起,使得![]() 、
、![]() 、
、![]() 、
、![]() 四点重合于一点
四点重合于一点![]() ,得到一个四棱锥.对于下面四个结论:
,得到一个四棱锥.对于下面四个结论:
①![]() 与
与![]() 为异面直线; ②直线
为异面直线; ②直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]()
③![]() 平面
平面![]() ; ④平面
; ④平面![]() 平面
平面![]() ;
;
其中正确结论的个数有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
【答案】D
【解析】①错误.所得四棱锥中,设![]() 中点为
中点为![]() ,则
,则![]() 、
、![]() 两点重合,∵
两点重合,∵![]() ,即
,即![]() ,即
,即![]() 与
与![]() 不是异面直线;②正确.∵
不是异面直线;②正确.∵![]() ,
, ![]() 与
与![]() 重合,且
重合,且![]() 与
与![]() 所成角为
所成角为![]() ,说明
,说明![]() 与
与![]() 所成角为
所成角为![]() ;③正确.∵
;③正确.∵![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ;④正确.∵
;④正确.∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() 点,∴平面
点,∴平面![]() 平面
平面![]() ,即平面
,即平面![]() 平面
平面![]() ,故选
,故选![]() .
.
【 方法点睛】本题主要通过对多个命题真假的判断,主要综合考查线线成角、线面成角、线面平行以及面面平行的判断,属于难题.这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,要注意从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】数列{an}满足a1=2,an+1=an2+6an+6(n∈N×)
(1)设Cn=log5(an+3),求证{Cn}是等比数列;
(2)求数列{an}的通项公式;
(3)设bn= ![]() ﹣
﹣ ![]() ,数列{bn}的前n项和为Tn , 求证:﹣
,数列{bn}的前n项和为Tn , 求证:﹣ ![]() ≤Tn<﹣
≤Tn<﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在直线3x+y﹣1=0上,且圆C在x轴、y轴上截得的弦长AB和MN分别为 ![]() 和
和 ![]() .
.
(1)求圆C的方程;
(2)若圆心C位于第四象限,点P(x,y)是圆C内一动点,且x,y满足 ![]() ,求
,求 ![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,角A、B、C的对边分别为a、b、c,已知a=2,A=45°,若三角形有两解,则边b的取值范围是( )
A.b>2
B.b<2
C.2<b<2 ![]()
D.2<b<2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )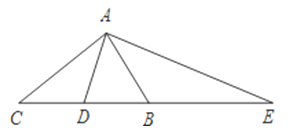
A.△AED∽△ACB
B.△AEB∽△ACD
C.△BAE∽△ACE
D.△AEC∽△DAC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系 ![]() 中,直线 的参数方程为
中,直线 的参数方程为  (
( ![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)写出圆 ![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 为直线
为直线 ![]() 上一动点,当
上一动点,当 ![]() 到圆心
到圆心 ![]() 的距离最小时,求
的距离最小时,求 ![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是公差不为零的等差数列,满足
是公差不为零的等差数列,满足![]() 数列
数列![]() 的通项公式为
的通项公式为![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)将数列![]() ,
,![]() 中的公共项按从小到大的顺序构成数列
中的公共项按从小到大的顺序构成数列![]() ,请直接写出数列
,请直接写出数列![]() 的通项公式;
的通项公式;
(3)记![]() ,是否存在正整数
,是否存在正整数![]()
![]() ,使得
,使得![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com