
 如图所示,某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点A、B,观察对岸的点C,测得∠CAB=105°,∠CBA=45°,且AB=100m.
如图所示,某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点A、B,观察对岸的点C,测得∠CAB=105°,∠CBA=45°,且AB=100m.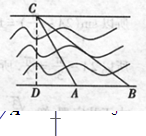
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||||
| 4 |
| AB |
| sin∠ACB |
| BC |
| sin∠CAB |
| ABsin105° |
| sin30° |
| 6 |
| 2 |
| 6 |
| 2 |
| ||
| 2 |
| 3 |
| ||||
| 4 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图所示,某学校的教学楼前有一块矩形空地ABCD,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为a米与b米均不小于2米,且要求“转角处(图中矩形AEFG)”的面积为8平方米
如图所示,某学校的教学楼前有一块矩形空地ABCD,其长为32米,宽为18米,现要在此空地上种植一块矩形草坪,三边留有人行道,人行道宽度为a米与b米均不小于2米,且要求“转角处(图中矩形AEFG)”的面积为8平方米查看答案和解析>>
科目:高中数学 来源: 题型:
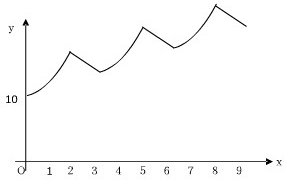 (2008•徐汇区二模)随着国民经济的日益发展和居民财富的不断积累,理财观念日益深入人心.投资股市正成为一种时尚,如图所示是某股票的K线图(即股票价格的走势图),其起始价格为每股10元.假设其运行规律为两个月上涨,接下来一个月下跌,上行线是以每月10%递增的指数型曲线段,下行线是以-1为斜率的直线型线段;设第n月末的股票价格为f(n).
(2008•徐汇区二模)随着国民经济的日益发展和居民财富的不断积累,理财观念日益深入人心.投资股市正成为一种时尚,如图所示是某股票的K线图(即股票价格的走势图),其起始价格为每股10元.假设其运行规律为两个月上涨,接下来一个月下跌,上行线是以每月10%递增的指数型曲线段,下行线是以-1为斜率的直线型线段;设第n月末的股票价格为f(n).查看答案和解析>>
科目:高中数学 来源:2013年高考数学复习卷B(二)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com