
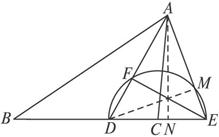
(1)求证:AF=DF;
(2)求∠AED的余弦值;
(3)如果BD=10,求△ABC的面积.
思路解析:根据题中角的关系进行转化,可证得AF=DF.并由勾股定理、切割线定理计算.
(1)证明:∵AD平分∠BAC,
∴∠BAD=∠DAC.
∵∠B=∠CAE,
∴∠BAD+∠B=∠DAC+∠CAE.
∵∠ADE=∠BAD+∠B,
∴∠ADE=∠DAE.
∴EA=ED.
∵DE是半圆C的直径,
∴∠DFE=90°.
∴AF=DF.
(2)解:连结DM,

∵DE是半圆C的直径,
∴∠DME=90°.
∵FE∶FD=4∶3,
∴可设FE=4x,则FD=3x.
由勾股定理,得DE=5x.
∴AE=DE=5x,AF=FD=3x.
由切割线定理的推论,得AF·AD=AM·AE.
∴3x(3x+3x)=AM·5x.
∴AM=![]() x.
x.
∴ME=AE-AM=5x-![]() x=
x=![]() x.
x.
在Rt△DME中,cos∠AED=![]() =
= .
.
(3)解:过A点作AN⊥BE于N,
由cos∠AED=![]() ,得sin∠AED=
,得sin∠AED=![]() .
.
∴AN=![]() ,AE=
,AE=![]() x.
x.
在△CAE和△ABE中,
∵∠CAE=∠B,∠AEC=∠BEA,
∴△CAE∽△ABE.
∴![]() ,即AE2=BE·CE.
,即AE2=BE·CE.
∴(5x)2=(10+5x)·![]() x.
x.
解得x=2.
∴AN=![]() x=
x=![]() ,BC=BD+DC=10+
,BC=BD+DC=10+![]() ×2=15.
×2=15.
∴S△ABC=![]() BC·AN=
BC·AN=![]() ×15×
×15×![]() =72.
=72.


科目:高中数学 来源: 题型:
| α |
| ||
|
|
| ||
|
|
| β |
| ||
|
| ||
|
|
| ||
|
|
| α |
| β |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com