练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    为了解某校高三学生的视力情况，随机抽查了该校名高三学生，得到如图所示的频率分布直方图．
    (1)求图中的值；
    (2)若从视力在的学生中随机选取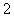人，求这2人视力均在的概率
    （1）；（2）.

    试题分析：（1）先从频率分布直方图中获得信息：组距为，进而由组距乘以每个小矩形的高可得相应的频率，由频率和为1进行计算即可得到的值；（2）先根据频率分布直方图的有关信息得到视力在的人数：人，其中有3人视力在，进而用穷举法列出6人选2人的所有情况共有15种，这两人恰好来自视力在内的情况共有3种，进而根据古典概型的概率计算公式，即可得到所求概率为.
    试题解析：(1)组距为，则，故
    (2)视力在和均有人，设视力在的3人分别用字母表示，视力在分别用字母表示，则随机选取的人所有可能如下：，共有15种不同的情况.而视力在的包含的结果为：，共有3种，其概率为.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

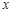    某种产品的广告费用支出（万元）与销售额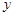（万元）之间有如下的对应数据：

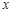    		2
    		4
    		5
    		6
    		8

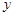    		30
    		40
    		60
    		50
    		70
    x
    		2
    		4
    		5
    		6
    		8
    y
    		30
    		40
    		60
    		50
    		70
     
    （1）画出散点图；
    （2）求回归直线方程；
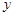    （3）据此估计广告费用为9万元时，销售收入的值．
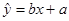    参考公式：回归直线的方程，其中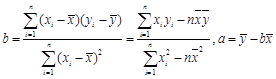
    ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

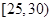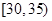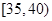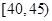    某单位N名员工参加“社区低碳你我他”活动，他们的年龄在25岁至50岁之间。按年龄分组：第1组，第2组，第3组，第4组，第5组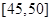，由统计的数据得到的频率分布直方图如图所示，在其右面的表是年龄的频率分布表。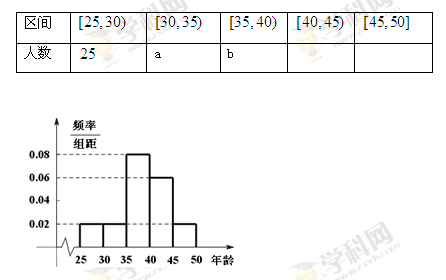

    （1）求正整数a，b，N的值；
    （2）现要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，则年龄在第1，2，3组中抽取的人数分别是多少？
    （3）在（2）的条件下，从这6人中随机抽取2人参加社区宣传交流活动，求恰有1 人在第3组的概率。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

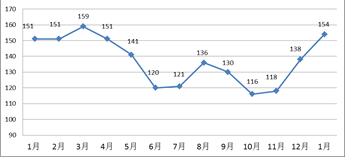
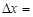    下图为某地区2012年1月到2013年1月鲜蔬价格指数的变化情况:

    记本月价格指数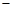上月价格指数.规定：当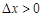时，称本月价格指数环比增长；
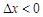    当时，称本月价格指数环比下降；当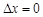时，称本月价格指数环比持平.
    （1） 比较2012年上半年与下半年鲜蔬价格指数月平均值的大小（不要求计算过程）；
    （2） 直接写出从2012年2月到2013年1月的12个月中价格指数环比下降的月份.若从这12个月中随机选择连续的两个月进行观察，求所选两个月的价格指数都环比下降的概率;
    （3）由图判断从哪个月开始连续三个月的价格指数方差最大.(结论不要求证明)

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    为预防X病毒爆发,某生物技术公司研制出一种X病毒疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个样本分成三组,测试结果如下表:
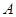    分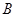组
    		组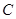
    		组
    		组
    疫苗有效
    		673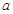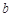


    疫苗无效
    		77
    		90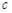

     
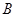    已知在全体样本中随机抽取1个，抽到组疫苗有效的概率是0．33．
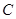    （1）现用分层抽样的方法在全体样本中抽取360个测试结果，应在组抽取样本多少个?
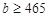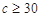    （2）已知，，求通过测试的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知方程y＝bx＋a是两个具有线性相关关系的变量的一组数据(x1，y1)，(x2，y2)，…，(x10，y10)的回归方程，则“，”是“(x0，y0)满足线性回归方程y＝bx＋a”的(　　)
    A．充分不必要条件 B．必要不充分条件
    C．充要条件 D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

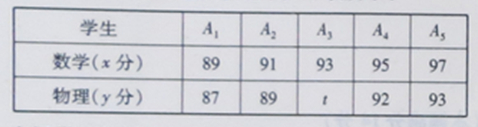
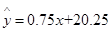    为研究学生物理成绩与数学成绩是否相关，某中学老师将一次考试中五名学生的数学、物理成绩记录如下表所示：

    根据上表提供的数据，经检验物理成绩与数学成绩呈线性相关，且得到y关于x的线性回归方程，那么表中t的值为       .

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    一个车间为了规定工时定额．需要确定加工零件所花费的时间，为此进行了10次试验．测得的数据如下：
    零件数x/个
    		10
    		20
    		30
    		40
    		50
    		60
    		70
    		80
    		90
    		100
    加工时间y/分
    		62
    		68
    		75
    		81
    		89
    		95
    		102
    		108
    		115
    		122
    (1)y与x是否具有线性相关关系？
    (2)如果y与x具有线性相关关系，求回归直线方程；
    (3)根据求出的回归直线方程，预测加工200个零件所用的时间为多少？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某观赏鱼池塘中养殖大量的红鲫鱼与金鱼,为了估计池中两种鱼数量情况,养殖人员从池中捕出红鲫鱼和金鱼各1000条,并给每条鱼作上不影响其存活的记号,然后放回池内,经过一段时间后,再从池中随机捕出1000条鱼,分别记录下其中有记号的鱼数目,再放回池中,这样的记录作了10次,将记录数据制成如图所示的茎叶图.

    (1)根据茎叶图分别计算有记号的两种鱼的平均数,并估计池塘中两种鱼的数量.
    (2)随机从池塘中逐条有放回地捕出3条鱼,求恰好是1条金鱼2条红鲫鱼的概率.

    查看答案和解析>>

    同步练习册答案