练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图是某学校高三年级的三个班在一学期内的六次数学测试的平均成绩y关于测试序号x的函数图象，为了容易看出一个班级的成绩变化，将离散的点用虚线连接，根据图象，给出下列结论：

    ①一班成绩始终高于年级平均水平，整体成绩比较好；

    ②二班成绩不够稳定，波动程度较大；

    ③三班成绩虽然多次低于年级平均水平，但在稳步提升.

    其中错误的结论的个数为（ ）

    A.0B.1C.2D.3

    【答案】A

    【解析】

    看图分析，①比较一班与年级平均成绩的大小；②看二班的成绩波动；③看三班的平均成绩，以及增减性，即可得到答案.

    由图可知，一班成绩始终高于年级平均水平，整体成绩比较好，故①正确；

    二班的成绩有时高于年级整体成绩，有时低于年级整体成绩，特别是第六次成绩远低于

    年级整体成绩，可知二班成绩不稳定，波动程度较大，故②正确；

    三班成绩虽然多数时间低于年级平均水平，只有第六次高于年级整体成绩，

    但在稳步提升，故③正确.

    ∴错误结论的个数为0.

    故选：A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数，世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段，可以用指数模型：描述累计感染病例数I(t)随时间t(单位:天)的变化规律，指数增长率r与R0，T近似满足R0 =1+rT.有学者基于已有数据估计出R0=3.28，T=6.据此，在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间约为(ln2≈0.69) （ ）

    A.1.2天B.1.8天

    C.2.5天D.3.5天

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，已知椭圆的左、右焦点分别为F1，F2，点A在椭圆E上且在第一象限内，AF2⊥F1F2，直线AF1与椭圆E相交于另一点B．

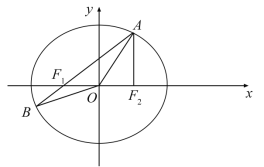
    （1）求△AF1F2的周长；

    （2）在x轴上任取一点P，直线AP与椭圆E的右准线相交于点Q，求的最小值；

    （3）设点M在椭圆E上，记△OAB与△MAB的面积分别为S1，S2，若S2=3S1，求点M的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若曲线在处切线的斜率为，判断函数的单调性；

    （2）若函数有两个零点，，证明，并指出a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数是定义在的偶函数，且.当时，，若方程有300个不同的实数根，则实数m的取值范围为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在棱长为1的正方体中，为棱上的动点（点不与点，重合），过点作平面分别与棱，交于，两点，若，则下列说法正确的是（ ）

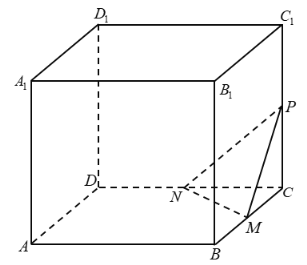
    A.面

    B.存在点，使得∥平面

    C.存在点，使得点到平面的距离为

    D.用过，，三点的平面去截正方体，得到的截面一定是梯形

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校课外兴趣小组利用假期到植物园开展社会实践活动，研究某种植物生长情况与温度的关系.现收集了该种植物月生长量y（cm）与月平均气温x（℃）的8组数据，并制成如图所示的散点图.

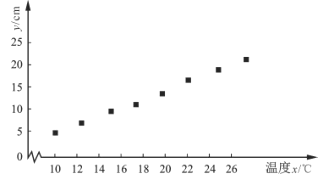
    根据收集到的数据，计算得到如下值：

    18

    12.325

    224.04

    235.96

    （1）求出y关于x的线性回归方程（最终结果的系数精确到0.01），并求温度为28℃时月生长量y的预报值；

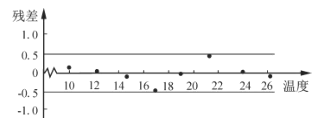
    （2）根据y关于x的回归方程，得到残差图如图所示，分析该回归方程的拟合效果.

    附：对于一组数据，其回归直线的斜率和截距的最小二乘估计分别为，.

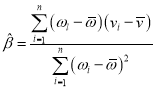    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为满足人民对美好生活的向往，环保部门要求相关企业加强污水治理，排放未达标的企业要限期整改，设企业的污水排放量W与时间t的关系为，用的大小评价在这段时间内企业污水治理能力的强弱，已知整改期内，甲、乙两企业的污水排放量与时间的关系如下图所示.


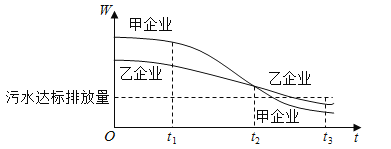
    给出下列四个结论：

    ①在这段时间内，甲企业的污水治理能力比乙企业强；

    ②在时刻，甲企业的污水治理能力比乙企业强；

    ③在时刻，甲、乙两企业的污水排放都已达标；

    ④甲企业在这三段时间中，在的污水治理能力最强．

    其中所有正确结论的序号是____________________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，三棱锥中，面面.

    （1）若，求证：面；

    （2）若，，，且和互余，求直线和面所成角的正弦值.

    查看答案和解析>>

    同步练习册答案