
【题目】有以下命题:
①存在实数![]() ,
,![]() ,使得
,使得![]() ;
;
②“![]() ,
,![]() ”的否定是“存在
”的否定是“存在![]() ,
,![]() ”;
”;
③掷一枚质地均匀的正方体骰子,向上的点数不小于3的概率为![]() ;
;
④在闭区间![]() 上取一个随机数
上取一个随机数![]() ,则
,则![]() 的概率为
的概率为![]() .
.
其中所有的真命题为________.(填写所有正确的结论序号)
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是方程
是方程![]() 的两个不等实数根,记
的两个不等实数根,记![]() (
(![]() ).下列两个命题( )
).下列两个命题( )
①数列![]() 的任意一项都是正整数;
的任意一项都是正整数;
②数列![]() 存在某一项是5的倍数.
存在某一项是5的倍数.
A.①正确,②错误B.①错误,②正确
C.①②都正确D.①②都错误
查看答案和解析>>
科目:高中数学 来源: 题型:
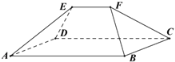
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍[chúméng]”的五面体(如图),四边形![]() 为矩形,棱
为矩形,棱![]() .若此几何体中,
.若此几何体中,![]() ,
,![]() 和
和![]() 都是边长为
都是边长为![]() 的等边三角形,则此几何体的体积为( )
的等边三角形,则此几何体的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第七届世界军人运动会于2019年10月18日至27日(共10天)在武汉召开,人们通过手机、电视等方式关注运动会盛况.某调查网站从观看运动会的观众中随机选出200人,经统计这200人中通过传统的传媒方式电视端口观看的人数与通过新型的传媒方式![]() 端口观看的人数之比为
端口观看的人数之比为![]() .将这200人按年龄分组:第1组
.将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() .其中统计通过传统的传媒方式电视端口观看的观众得到的频率分布直方图如图所示.
.其中统计通过传统的传媒方式电视端口观看的观众得到的频率分布直方图如图所示.
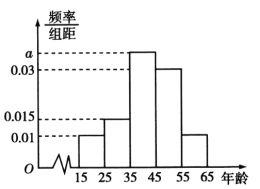
(1)求![]() 的值及通过传统的传媒方式电视端口观看的观众的平均年龄;
的值及通过传统的传媒方式电视端口观看的观众的平均年龄;
(2)把年龄在第1,2,3组的观众称为青少年组,年龄在第4,5组的观众称为中老年组,若选出的200人中通过新型的传媒方式![]() 端口观看的中老年人有12人,请完成下面
端口观看的中老年人有12人,请完成下面![]() 列联表,则能否在犯错误的概率不超过0.1的前提下认为观看军人运动会的方式与年龄有关?
列联表,则能否在犯错误的概率不超过0.1的前提下认为观看军人运动会的方式与年龄有关?
通过 | 通过电视端口观看军人运动会 | 合计 | |
青少年 | |||
中老年 | |||
合计 |
span>
附: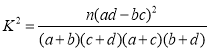 (其中
(其中![]() ).
).
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)[选修4-5:不等式选讲]
已知函数![]() =|x-a|+
=|x-a|+![]() (a≠0)
(a≠0)
(1)若不等式![]() -
-![]() ≤1恒成立,求实数m的最大值;
≤1恒成立,求实数m的最大值;
(2)当a<![]() 时,函数g(x)=
时,函数g(x)=![]() +|2x-1|有零点,求实数a的取值范围
+|2x-1|有零点,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 与圆
与圆![]() 在第一象限交点为
在第一象限交点为![]() ,曲线
,曲线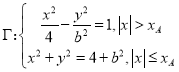 .
.
(1)若![]() ,求b;
,求b;
(2)若![]() ,
,![]() 与x轴交点是
与x轴交点是![]() ,P
,P![]() 是曲线
是曲线![]() 上一点,且在第一象限,并满足
上一点,且在第一象限,并满足![]() ,求∠
,求∠![]() ;
;
(3)过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于M、N两点,用b的代数式表示
于M、N两点,用b的代数式表示![]() ,并求出
,并求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下命题:
(1)已知回归直线方程为![]() ,样本点的中心为
,样本点的中心为![]() ,则
,则![]() ;
;
(2)已知![]() ,
,![]() 与
与![]() 的夹角为钝角,则
的夹角为钝角,则![]() 是
是![]() 的充要条件;
的充要条件;
(3)函数![]() 图象关于点
图象关于点![]() 对称且在
对称且在![]() 上单调递增;
上单调递增;
(4)命题“存在![]() ”的否定是“对于任意
”的否定是“对于任意![]() ”;
”;
(5)设函数![]() ,若函数
,若函数![]() 恰有三个零点,则实数m的取值范围为
恰有三个零点,则实数m的取值范围为![]() .
.
其中不正确的命题序号为______________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() ,
,![]() ,
,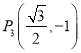 ,
,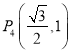 四点中恰有三点在椭圆
四点中恰有三点在椭圆![]() 上,抛物线
上,抛物线![]() 焦点到准线的距离为
焦点到准线的距离为![]() .
.
(1)求椭圆![]() 、抛物线
、抛物线![]() 的方程;
的方程;
(2)过椭圆![]() 右顶点Q的直线
右顶点Q的直线![]() 与抛物线
与抛物线![]() 交于点A、B,射线
交于点A、B,射线![]() 、
、![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() 、
、![]() .
.
(i)证明:![]() 为定值;
为定值;
(ii)记![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com