
【题目】已知函数f(x)=4cos ωx·sin![]() +a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
(1)求a和ω的值;
(2)求函数f(x)在[0,π]上的单调递减区间.
【答案】(1)a=-1. ω=1.(2)![]() .
.
【解析】
(1)先由三角的两角和的正弦公式得到函数表达式,再由最大值为当sin![]() =1时,f(x)取得最大值2+1+a=3+a,求出a即可,由图像得到f(x)图象上相邻两个最高点的距离为π,进而得到周期和ω=1;(2)f(x)=sin
=1时,f(x)取得最大值2+1+a=3+a,求出a即可,由图像得到f(x)图象上相邻两个最高点的距离为π,进而得到周期和ω=1;(2)f(x)=sin![]() ,根据由
,根据由![]() +2kπ≤
+2kπ≤![]() ≤
≤![]() +2kπ,解出x的范围得到单调递减区间.
+2kπ,解出x的范围得到单调递减区间.
(1)f(x)=4cosωx·sin![]() +a
+a
=4cosωx·![]() +a
+a
=2![]() sinωxcos ωx+2cos2ωx-1+1+a
sinωxcos ωx+2cos2ωx-1+1+a
=![]() sin2ωx+cos 2ωx+1+a
sin2ωx+cos 2ωx+1+a
=2sin![]() +1+a.
+1+a.
当sin![]() =1时,f(x)取得最大值2+1+a=3+a.
=1时,f(x)取得最大值2+1+a=3+a.
又f(x)最高点的纵坐标为2,∴3+a=2,即a=-1.
又f(x)图象上相邻两个最高点的距离为π,
∴f(x)的最小正周期为T=π,
∴2ω=![]() =2,ω=1.
=2,ω=1.
(2)由(1)得f(x)=2sin![]() ,
,
由![]() +2kπ≤2x+
+2kπ≤2x+![]() ≤
≤![]() +2kπ,k∈Z,
+2kπ,k∈Z,
得![]() +kπ≤x≤
+kπ≤x≤![]() +kπ,k∈Z.
+kπ,k∈Z.
令k=0,得![]() ≤x≤
≤x≤![]() .
.
∴函数f(x)在[0,π]上的单调递减区间为![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】某单位响应党中央“精准扶贫”号召,对某村6户贫困户中的甲户进行定点帮扶,每年跟踪调查统计一次,从2015年1月1日至2018年12月底统计数据如下(人均年纯收入):
年份 | 2015年 | 2016年 | 2017年 | 2018年 |
年份代码 | 1 | 2 | 3 | 4 |
收入 | 25 | 28 | 32 | 35 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计甲户在2019年能否脱贫;(国家规定2019年脱贫标准:人均年纯收入为3747元)
,并估计甲户在2019年能否脱贫;(国家规定2019年脱贫标准:人均年纯收入为3747元)
(2)2019年初,根据扶贫办的统计知,该村剩余5户贫困户中还有2户没有脱贫,现从这5户中抽取2户,求至少有一户没有脱贫的概率.
参考公式: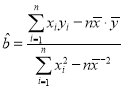 ,
,![]() ,其中
,其中![]() ,
,![]() 为数
为数![]() ,
,![]() 的平均数.
的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义域为R的奇函数.
是定义域为R的奇函数.
(1)求实数k的值;
(2)若![]() ,试判断函数
,试判断函数![]() 的单调性,并求不等式
的单调性,并求不等式![]() 的解集;
的解集;
(3)若![]() ,设
,设![]() ,
,![]() 在
在![]() 上的最小值为-1,求实数m的值.
上的最小值为-1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,AB=2BC=2,E为CD中点,以BE为折痕将△BEC折起,使C到C′的位置,且平面BEC′⊥平面ABED.

(1)求证:BC′⊥AE;
(2)求空间四边形ABC′E的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·龙泉驿区一中]交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,且保费与上一年车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,且保费与上一年车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
交强险浮动因素和费率浮动比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮 |
| 上两个年度未发生有责任道路交通事故 | 下浮 |
| 上三个以及以上年度未发生有责任道路交通事故 | 下浮 |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮 |
| 上一个年度发生有责任道路交通死亡事故 | 上浮 |
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了70辆车龄已满三年该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 13 | 7 | 20 | 14 | 6 |
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损6000元,一辆非事故车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有7辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选2辆,求这2辆车恰好有一辆为事故车的概率;
②若该销售商一次性购进70辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值(结果用分数表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,阅读如图所示的程序框图,若输入的
,阅读如图所示的程序框图,若输入的![]() 的值为
的值为![]() ,输出的
,输出的![]() 的值恰为直线
的值恰为直线![]() 在
在![]() 轴上的截距,且
轴上的截距,且![]() .
.

(1)求直线![]() 与
与![]() 的交点坐标;
的交点坐标;
(2)若直线![]() 过直线
过直线![]() 与
与![]() 的交点,且在
的交点,且在![]() 轴上的截距是在
轴上的截距是在![]() 轴上的截距的2倍,求
轴上的截距的2倍,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣1)|x﹣a|﹣x﹣2a(x∈R).
(1)若a=﹣1,求方程f(x)=1的解集;
(2)若![]() ,试判断函数y=f(x)在R上的零点个数.
,试判断函数y=f(x)在R上的零点个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com