
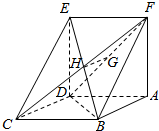
 如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点,记CD=x,V(x)表示四棱锥F-ABCD的体积.
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点,记CD=x,V(x)表示四棱锥F-ABCD的体积.分析 (1)由于FA⊥AD,平面ADEF⊥平面ABCD,可得FA⊥平面ABCD.由于BC=2,BD⊥CD,CD=x,可得DB=$\sqrt{4-{x}^{2}}$(0<x<2).∴S平行四边形ABCD=2S△BCD.即可得出V(x)=$\frac{1}{3}{S}_{平行四边形ABCD}•FA$.
(2)由基本不等式的性质即可得出.
解答 解:(1)∵四边形ADEF为正方形,∴FA⊥AD,
又∵平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,
∴FA⊥平面ABCD.
∵BC=2,BD⊥CD,CD=x,
∴DB=$\sqrt{4-{x}^{2}}$(0<x<2).
∴S平行四边形ABCD=2S△BCD=2×$\frac{1}{2}x\sqrt{4-{x}^{2}}$=$x\sqrt{4-{x}^{2}}$.
∴V(x)=$\frac{1}{3}{S}_{平行四边形ABCD}•FA$=$\frac{1}{3}x\sqrt{4-{x}^{2}}×2$=$\frac{2}{3}x\sqrt{4-{x}^{2}}$.(0<x<2).
(2)由基本不等式的性质可得:V(x)$≤\frac{2}{3}$$•\frac{{x}^{2}+(4-{x}^{2})}{2}$=$\frac{4}{3}$,当且仅当$x=\sqrt{4-{x}^{2}}$,即x=$\sqrt{2}$时取等号.
∴V(x)的最大值是$\frac{4}{3}$.
点评 本题考查了线面面面垂直的判定与性质定理、四棱锥的体积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | a>b>c | C. | a>c>b | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | (-∞,1] | C. | [-1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{\sqrt{15}}{5}$ | D. | $\frac{{\sqrt{14}}}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com