数列{an}满足a1=a,a2=-a(a>0),且{an}从第二项起是公差为6的等差数列,Sn是{an}的前n项和.
(1)当n≥2时,用a与n表示an与Sn;
(2)若在S6与S7两项中至少有一项是Sn的最小值,试求a的取值范围;
(3)若a为正整数,在(2)的条件下,设Sn取S6为最小值的概率是p1,Sn取S7为最小值的概率是p2,比较p1与p2的大小.
解:(1)由已知,当n≥2时,a
n=-a+6(n-2),
即a
n=6n-(a+12).
∴S
n=a
1+a
2+a
3++a
n=a+(n-1)(-a)+
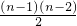
•6=3n
2-(a+9)n+2a+6.
(2)由已知,当n≥2时,{a
n}是等差数列,公差为6,数列递增.
若S
6是S
n的最小值,则
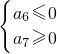
即
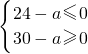
∴24≤a≤30.
若S
7是S
n的最小值,则
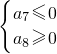
即
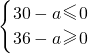
∴30≤a≤36.
∴当S
6与S
7两项中至少有一项是S
n的最小值时,a的取值范围是[24,36].
(3)∵a是正整数,由(2)知,a=24,25,26,,36.
当S
6是S
n最小值时,a=24,25,26,27,28,29,30
当S
7是S
n最小值时,a=30,31,32,33,34,35,36
∴p
1=p
2=
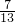
.
分析:(1)因为数列是等差数列,所以由通项公式和前n项和公式求解.
(2)由 (1)知:{a
n}是等差数列,且公差为6,所以数列递增,如果S
6是S
n的最小值,则有
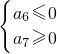
,若S
7是S
n的最小值,则有
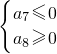
两种情况最后取并集.
(3)由“a是正整数”,则本题是一个古典概型,由(2)知,a的所以取值为:24,25,26,…,36.当S
6是S
n最小值时,a的取值为:24,25,26,27,28,29,30,当S
7是S
n最小值时,a的取值为:30,31,32,33,34,35,36,由概率公式求得p
1,p
2再比较.
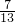
.
点评:本题主要考查等差数列的通项及前n项和公式以及用通项法研究前n和最值问题,同时,还渗透了概率问题,综合性较强,转化比较灵活,要求比较高.

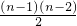 •6=3n2-(a+9)n+2a+6.
•6=3n2-(a+9)n+2a+6.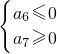 即
即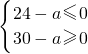
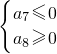 即
即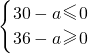
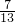 .
.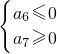 ,若S7是Sn的最小值,则有
,若S7是Sn的最小值,则有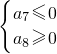 两种情况最后取并集.
两种情况最后取并集.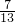 .
.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案