
【题目】在如图所示的多面体![]() 中,
中,![]() ,且
,且![]() ,四边形
,四边形![]() 为正方形,
为正方形,![]() 为等边三角形,平面
为等边三角形,平面![]() 平面
平面![]() .
.

(1)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)分别取![]() 的中点
的中点![]() ,连接
,连接![]() ,由
,由![]() ,得
,得![]() ,根据平面
,根据平面![]() 平面
平面![]() ,得到
,得到![]() 平面
平面![]() .然后以
.然后以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,求得向量
轴,建立空间直角坐标系,求得向量![]() 的坐标,代入线线角的向量公式
的坐标,代入线线角的向量公式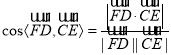 求解.
求解.
(2)在(1)的坐标系下,分别求得平面![]() 和平面
和平面![]() 的一个法向量为,代入面面角的向量公式
的一个法向量为,代入面面角的向量公式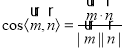 求解.
求解.
分别取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
因为![]() ,所以
,所以![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() ,且
,且![]() ,
,
所以![]() ,且
,且![]() ,
,
则四边形![]() 为平行四边形,故
为平行四边形,故![]() ,
,
所以![]() 平面
平面![]() .
.
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,
轴,
建立如图所示的空间直角坐标系![]() .
.
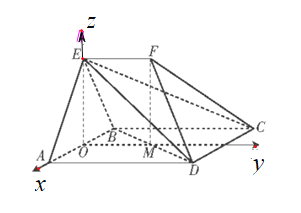
由题意可得![]() ,
,
(1)因为![]() ,
,
所以![]() ,
,
则异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(2)![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则 ,即
,即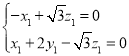 ,
,
令![]() ,得
,得![]() .于是
.于是![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则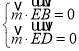 ,即
,即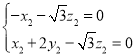 ,令
,令![]() ,得
,得![]() .
.
于是![]() .
.
所以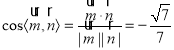 .
.
所以二面角![]() 的正弦值为
的正弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,设直线
,设直线![]() 过椭圆
过椭圆![]() 的上顶点和右顶点,坐标原点
的上顶点和右顶点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)过点![]() 且斜率不为零的直线
且斜率不为零的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,在
两点,在![]() 轴的正半轴上是否存在定点
轴的正半轴上是否存在定点![]() ,使得直线
,使得直线![]() ,
,![]() 的斜率之积为非零的常数?若存在,求出定点
的斜率之积为非零的常数?若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“工资条里显红利,个税新政人民心”.随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.2019年1月1日实施的个税新政主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除;(3)专项附加扣除包括住房、子女教育和赡养老人等.
新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
缴税级数 | 每月应纳税所得额(含税)=收入-个税起征点 | 税率(%) | 每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除 | 税率(%) |
1 | 不超过1500元部分 | 3 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元部分 | 10 | 超过3000元至12000元部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元至55000元部分 | 30 | 超过35000元至55000元部分 | 30 |
··· | ··· | ··· | ··· | ··· |
随机抽取某市1000名同一收入层级的![]() 从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等。
从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等。
假设该市该收入层级的![]() 从业者都独自享受专项附加扣除,将预估的该市该收入层级的
从业者都独自享受专项附加扣除,将预估的该市该收入层级的![]() 从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
(1)设该市该收入层级的![]() 从业者2019年月缴个税为
从业者2019年月缴个税为![]() 元,求
元,求![]() 的分布列和期望;
的分布列和期望;
(2)根据新旧个税方案,估计从2019年1月开始,经过多少个月,该市该收入层级的![]() 从业者各月少缴交的个税之和就超过2019年的月收入?
从业者各月少缴交的个税之和就超过2019年的月收入?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举办了一场主题为“爱诗词、爱祖国”的诗词知识竞赛,从参赛的全体学生中抽出30人的成绩作为样本.对这30名学生的成绩进行统计,并按![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分组,得到如图所示的频率分布直方图.
分组,得到如图所示的频率分布直方图.
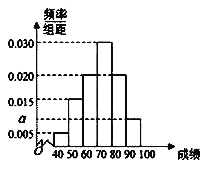
(1)求图中实数![]() 的值;
的值;
(2)估计参加这次知识竞赛的学生的平均成绩及成绩的中位数(平均成绩用每组中点值做代表,结果均保留一位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四种说法:
①四个实数![]() 依次成等比数列的必要而不充分条件是
依次成等比数列的必要而不充分条件是![]() .
.
②命题“若![]() 且
且![]() ,则
,则![]() ”为假命题.
”为假命题.
③若![]() 为假命题,则
为假命题,则![]() 均为假命题.
均为假命题.
④若数列![]() 的前项n和
的前项n和![]() ,则该数列的通项公式
,则该数列的通项公式![]() .
.
其中正确说法的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲船在岛![]() 的正南
的正南![]() 处,以4千米/时的速度向正北方向航行,
处,以4千米/时的速度向正北方向航行,![]() 千米,同时乙船自岛
千米,同时乙船自岛![]() 出发以6千米/时向北偏东60°的方向驶去.当甲、乙两船相距最近时,它们所航行的时间为( )
出发以6千米/时向北偏东60°的方向驶去.当甲、乙两船相距最近时,它们所航行的时间为( )
A.![]() B.
B.![]() C.
C.![]() D.2.15h
D.2.15h
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理中是演绎推理的为( )
A. 由金、银、铜、铁可导电,猜想:金属都可导电
B. 猜想数列![]() 的通项公式为
的通项公式为![]()
C. 半径为![]() 的圆的面积
的圆的面积![]() ,则单位圆的面积
,则单位圆的面积![]()
D. 由平面直角坐标系中圆的方程为![]() ,推测空间直角坐标系中球的方程为
,推测空间直角坐标系中球的方程为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com