
【题目】已知函数f(x)=x2+2x|x﹣a|,其中a∈R.
(1)当a=﹣1时,在所给坐标系中作出f(x)的图象;
(2)对任意x∈[1,2],函数g(x)=﹣x+14的图象恒在函数f(x)图象的上方,求实数a的取值范围. 
【答案】
(1)解:当a=﹣1时,作出函数f(x)=x2+2x|x﹣a|=x2+2x|x+1|= ![]() 的图象,
的图象,
如图所示:
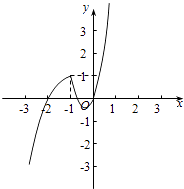
(2)解:由题意,对任意x∈[1,2],f(x)<g(x),
即f(x)+x<14恒成立,
只需[f(x)+x)]max<14.
另一方面,f(x)= ![]() .
.
当a≥0时,f(x)在(﹣∞,a)和(a,+∞)上均递增,∵f(a)=a2,则f(x)在R上递增,
当a<0时,f(x)在(﹣∞,a)和( ![]() ,+∞)上递增,在(a,
,+∞)上递增,在(a, ![]() )上递减,
)上递减,
故f(x)在x∈[1,2]上恒单调递增,从而y=f(x)+x在x∈[1,2]上也恒单调递增,
则[f(x)+x]max=f(2)+2=4+4|2﹣a|+2<14,即|2﹣a|<2,解得0<a<4,
故实数a的取值范围是(0,4)
【解析】(1)当a=﹣1时,作出函数f(x)=x2+2x|x+1|= ![]() 的图象.(Ⅱ)由题意,对任意x∈[1,2],只需[f(x)+x]max<14.分类讨论求得[f(x)+x]max , 可得实数a的取值范围.
的图象.(Ⅱ)由题意,对任意x∈[1,2],只需[f(x)+x]max<14.分类讨论求得[f(x)+x]max , 可得实数a的取值范围.


科目:高中数学 来源: 题型:
【题目】如图,棱长为a的正方体ABCD﹣A1B1C1D1中,点M,N,E分别是棱A1B1 , A1D1 , C1D1的中点. 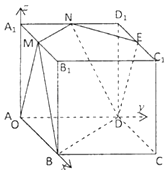
(1)过AM作一平面,使其与平面END平行(只写作法,不需要证明);
(2)在如图的空间直角坐标系中,求直线AM与平面BMND所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A=B=R,x∈A,y∈B,f:x→y=ax+b是从A到B的映射,若1和8的原象分别是3和10,则5在f下的象是( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点的动直线l与圆C1:x2+y2﹣6x+5=0相交于不同的两点A,B.
(1)求圆C1的圆心坐标;
(2)求线段AB 的中点M的轨迹C的方程;
(3)是否存在实数 k,使得直线L:y=k(x﹣4)与曲线 C只有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于下列命题,正确的个数是( )
①若点(2,1)在圆x2+y2+kx+2y+k2﹣15=0外,则k>2或k<﹣4
②已知圆M:(x+cosθ)2+(y﹣sinθ)2=1,直线y=kx,则直线与圆恒相切
③已知点P是直线2x+y+4=0上一动点,PA、PB是圆C:x2+y2﹣2y=0的两条切线,A、B是切点,则四边形PACB的最小面积是为2
④设直线系M:xcosθ+ysinθ=2+2cosθ,M中的直线所能围成的正三角形面积都等于12 ![]() .
.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得 ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(Ⅱ)判断变量x与y之间是正相关还是负相关;
(Ⅲ)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中, 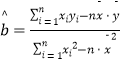 ,
, ![]() ,其中
,其中 ![]() ,
, ![]() 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为实常数.
为实常数.
(1)设![]() ,当
,当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,直线
时,直线![]() 、
、![]() 与函数
与函数![]() 的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.求证:
的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
1)已知两平面的法向量分别为 ![]() =(0,1,0),
=(0,1,0), ![]() =(0,1,1),则两平面所成的二面角为45°或135°;
=(0,1,1),则两平面所成的二面角为45°或135°;
2)若曲线 ![]() +
+ ![]() =1表示双曲线,则实数k的取值范围是(﹣∞,﹣4)∪(1,+∞);
=1表示双曲线,则实数k的取值范围是(﹣∞,﹣4)∪(1,+∞);
3)已知双曲线方程为x2﹣ ![]() =1,则过点P(1,1)可以作一条直线l与双曲线交于A,B两点,使点P是线段AB的中点.
=1,则过点P(1,1)可以作一条直线l与双曲线交于A,B两点,使点P是线段AB的中点.
其中正确命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com