
分析 由题意知F(-c,0),A(a,0),B(0,b);从而写出$\overrightarrow{BF}$=(-c,-b),$\overrightarrow{BA}$=(a,-b),从而可得-ac+a2-c2=0,从而可得$\frac{c}{a}$=$\frac{\sqrt{5}-1}{2}$;即sin∠OBF=$\frac{\sqrt{5}-1}{2}$,从而利用二倍角公式即可.
解答 解:由题意得,
F(-c,0),A(a,0),B(0,b);
∵$\overrightarrow{BF}$=(-c,-b),$\overrightarrow{BA}$=(a,-b),
∵BF⊥BA,
∴$\overrightarrow{BF}$•$\overrightarrow{BA}$=-ac+b2=0,
∴-ac+a2-c2=0,
解得,a=$\frac{1+\sqrt{5}}{2}$c,
故$\frac{c}{a}$=$\frac{2}{1+\sqrt{5}}$=$\frac{\sqrt{5}-1}{2}$;
故sin∠OBF=$\frac{\sqrt{5}-1}{2}$,
故cos2∠OBF=1-2•($\frac{\sqrt{5}-1}{2}$)2=$\sqrt{5}$-2,
故答案为:$\sqrt{5}$-2.
点评 本题考查了椭圆的性质的应用及平面向量的应用,同时考查了三角恒等变换的应用.


科目:高中数学 来源: 题型:选择题
| A. | m | B. | m2+1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知P是双曲线$\frac{{x}^{2}}{3}$-y2=1上任意一点,过点P分别作曲线的两条渐近线的垂线,垂足分别为A、B,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的值是( )
已知P是双曲线$\frac{{x}^{2}}{3}$-y2=1上任意一点,过点P分别作曲线的两条渐近线的垂线,垂足分别为A、B,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的值是( )| A. | -$\frac{3}{8}$ | B. | $\frac{3}{16}$ | C. | -$\frac{\sqrt{3}}{8}$ | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21 | B. | 20 | C. | 25 | D. | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
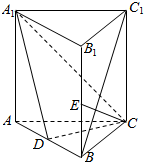 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点.
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com