
【题目】如果存在常数a,使得数列{an}满足:若x是数列{an}中的一项,则a-x也是数列{an}中的一项,称数列{an}为“兑换数列”,常数a是它的“兑换系数”.
(1)若数列:2,3,6,m(m>6)是“兑换系数”为a的“兑换数列”,求m和a的值;
(2)已知有穷等差数列{bn}的项数是n0(n0≥3),所有项之和是B,求证:数列{bn}是“兑换数列”,并用n0和B表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列{cn},是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
【答案】(1)a=9,m=7;(2)见解析;(3)见解析
【解析】
(1)利用“兑换数列”的定义得到a-m=2,a-6=3,即a=9,m=7.(2)利用“兑换数列”的定义可证明数列{bn}是“兑换数列”, 又因为数列{bn}所有项之和是B,所以B=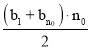 =
=![]() ,即a=
,即a=![]() ;(3)假设存在这样的等比数列{cn},设它的公比为q(q>1),通过推理得到q=1,与q>1矛盾,故不存在满足条件的数列{cn}.
;(3)假设存在这样的等比数列{cn},设它的公比为q(q>1),通过推理得到q=1,与q>1矛盾,故不存在满足条件的数列{cn}.
(1)解:因为2,3,6,m(m>6)是“兑换系数”为a的“兑换数列”
所以a-m,a-6,a-3,a-2也是该数列的项,且a-m<a-6<a-3<a-2,
故a-m=2,a-6=3,即a=9,m=7.
(2)证明:设数列{bn}的公差为d,
因为数列{bn}是项数为n0项的有穷等差数列
若b1≤b2≤b3≤…≤![]() ,则a-b1≥a-b2≥a-b3≥…≥a-
,则a-b1≥a-b2≥a-b3≥…≥a-![]() ,
,
即对数列{bn}中的任意一项bi(1≤i≤n0),a-bi=b1+(n0-i)d=![]() +1-i∈{bn}
+1-i∈{bn}
同理可得:b1≥b2≥b3≥…≥![]() ,a-bi=b1+(n0-i)d=
,a-bi=b1+(n0-i)d=![]() +1-i∈{bn}也成立,
+1-i∈{bn}也成立,
由“兑换数列”的定义可知,数列{bn}是“兑换数列”;
又因为数列{bn}所有项之和是B,所以B=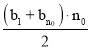 =
=![]() ,即a=
,即a=![]() ;
;
(3)解:假设存在这样的等比数列{cn},设它的公比为q(q>1),
因为数列{cn}为递增数列,所以c1<c2<c3<…<cn,则a-c1>a-c2>a-c3>…>a-cn,
又因为数列{cn}为“兑换数列”,则a-ci∈{cn},所以a-ci是正整数
故数列{cn}必为有穷数列,不妨设项数为n项,则ci+cn+1-i=a(1≤i≤n)
①若n=3,则有c1+c3=a,c2=![]() ,又c22=c1c3,由此得q=1,与q>1矛盾
,又c22=c1c3,由此得q=1,与q>1矛盾
②若n≥4,由c1+cn=c2+cn-1,得c1-c1q+c1qn-1-c1qn-2=0
即(q-1)(1-qn-2)=0,故q=1,与q>1矛盾;
综合①②得,不存在满足条件的数列{cn}.


科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,EA⊥平面ABCD,四边形ABCD为等腰梯形,![]() ,且
,且![]() ,AD=AE=1,∠ABC=60°,EF=
,AD=AE=1,∠ABC=60°,EF=![]() AC,且EF
AC,且EF![]() AC.
AC.
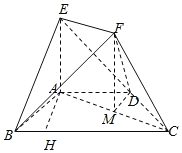
(Ⅰ)证明:AB⊥CF;
(Ⅱ)求二面角B﹣EF﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln![]() +ax﹣1(a≠0).
+ax﹣1(a≠0).
(I)求函数f(x)的单调区间;
(Ⅱ)已知g(x)+xf(x)=﹣x,若函数g(x)有两个极值点x1,x2(x1<x2),求证:g(x1)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() 的左、右点分别为
的左、右点分别为![]() 点
点 在椭圆上,且
在椭圆上,且![]()
(1)求椭圆![]() 的方程;
的方程;
(2)过点(1,0)作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于M、N两点,若
于M、N两点,若![]() 求直线
求直线![]() 的方程;
的方程;
(3)点P、Q为椭圆上的两个动点,![]() 为坐标原点,若直线
为坐标原点,若直线![]() 的斜率之积为
的斜率之积为![]() 求证:
求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
:![]() ,左顶点为
,左顶点为![]() ,经过点
,经过点![]() ,过点
,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
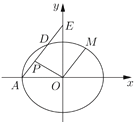
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为
为![]() 的中点,
的中点,![]() ,证明:对于任意的
,证明:对于任意的![]() 都有
都有![]() 恒成立;
恒成立;
(3)若过点![]() 作直线
作直线![]() 的平行线交椭圆
的平行线交椭圆![]() 于点
于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 统计学中将
统计学中将![]() 个数
个数![]() 的和记作
的和记作![]()
(1)设![]()
![]() ,求
,求![]() ;
;
(2)是否存在互不相等的非负整数![]() ,
,![]() ,使得
,使得![]() 成立,若存在,请写出推理的过程;若不存在请证明;
成立,若存在,请写出推理的过程;若不存在请证明;
(3)设![]()
![]() 是不同的正实数,
是不同的正实数,![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,判断
,判断![]() 是否为一个等比数列,请说明理由.
是否为一个等比数列,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人分别投掷两颗骰子与一颗骰子,设甲的两颗骰子的点数分别为![]() 与
与![]() ,乙的骰子的点数为
,乙的骰子的点数为![]() ,则掷出的点数满足
,则掷出的点数满足![]() 的概率为________(用最简分数表示).
的概率为________(用最简分数表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社会机构为了调查对手机游戏的兴趣与年龄的关系,通过问卷调查,整理数据得如下![]() 列联表:
列联表:

(1)根据列联表,能否有![]() 的把握认为对手机游戏的兴趣程度与年龄有关?
的把握认为对手机游戏的兴趣程度与年龄有关?
(2)若已经从40岁以上的被调查者中用分层抽样的方式抽取了10名,现从这10名被调查者中随机选取3名,记这3名被选出的被调查者中对手机游戏很有兴趣的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:![]()
参考数据:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com