练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

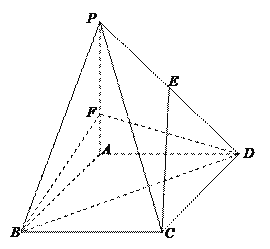
    【题目】如图，在边长为3的菱形ABCD中，∠ABC=60°，平面ABCD，且，E为PD中点，F在棱PA上，且.

    （1）求证：CE∥平面BDF；

    （2）求点P到平面BDF的距离.

    【答案】（1）见解析;（2）.

    【解析】试题分析：

    (1)利用题意取PF中点G，连接AC交BD于O点，连接FO，GC，EG

    由题意易知平面EGC∥平面BDF， ，∴CE∥平面BDF

    (2)由题意利用体积相等，在四面体FABD中，易求得， ，∴P到平面BDF的距离等于

    试题解析：

    （1）

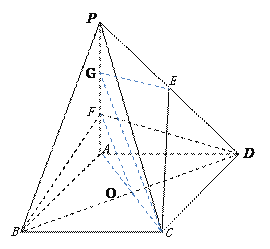
    取PF中点G，连接AC交BD于O点，连接FO，GC，EG

    由题意易知G为PF中点，又E为PD中点，所以GE∥FD，故

    FO为三角形AGC的中位线，所以FO∥GC

    所以面EGC∥平面BDF， ，∴CE∥平面BDF

    （2）由题意知点P到平面BDF的距离等于A到平面BDF的距离的两倍，记A到平面BDF的距离为h，则在四面体FABD中，易求得

    由体积自等得，

    ∴，∴P到平面BDF的距离等于

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列正确命题有__________．

    ①“”是“”的充分不必要条件

    ②如果命题“”为假命题，则中至多有一个为真命题

    ③设，若，则的最小值为

    ④函数在上存在，使，则a的取值范围或.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位共有老、中、青职工430人,其中青年职工160人，中年职工人数是老年职工人数的2倍。为了解职工身体状况，现采用分层抽样方法进行调查，在抽取的样本中有青年职工32人，则该样本中的老年职工人数为

    A. 9 B. 18 C. 27 D. 36

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆，圆与轴交于两点，过点的圆的切线为是圆上异于的一点，垂直于轴，垂足为，是的中点，延长分别交于．

    （1）若点，求以为直径的圆的方程，并判断是否在圆上；

    （2）当在圆上运动时，证明：直线恒与圆相切．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于函数，有下列结论：

    ①的最大值为；

    ②的最小正周期是；

    ③在区间上是减函数；

    ④直线是函数的一条对称轴方程.

    其中正确结论的序号是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆，直线经过点A (1，0).

    （1）若直线与圆C相切，求直线的方程；

    （2）若直线与圆C相交于P，Q两点，求三角形CPQ面积的最大值，并求此时直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在研究色盲与性别的关系调查中，调查了男性480人，其中有38人患色盲，调查的520个女性中6人患色盲．　

    （Ⅰ）根据题中数据建立一个的列联表；

    （Ⅱ）在犯错误的概率不超过0.001的前提下，能否认为“性别与患色盲有关系”？

    附：参考公式，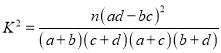

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在透明塑料制成的长方体容器内灌进一些水（未满），现将容器底面一边固定在底面上，再将容器倾斜，随着倾斜度的不同，有下列四种说法：

    ①水的部分始终呈棱柱状；

    ②水面四边形的面积为定值；

    ③棱始终与水面平行；

    ④若， ，则是定值.

    则其中正确命题的个数的是（ ）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， .

    （Ⅰ）若是奇函数，且在区间上是增函数，求的值；

    （Ⅱ）设，若在区间内有两个不同的零点， ，求的取值范围，并求的值.

    查看答案和解析>>

    同步练习册答案