
分析 (1)圆心(3,4)到l1的距离$d=\frac{{|{2k-4}|}}{{\sqrt{1+{k^2}}}}<4$,解出即可得出.
(2)直线l1:kx-y-k=0恒过定点(1,0),所以点A的坐标为(1,0),如图所示:将l1方程代入圆方程,
整理得(1+k)2x2-[6+2k(k+4)]•x+k2+8k+9=0.由韦达定理和中点的坐标公式可得M坐标.解方程组$\left\{{\begin{array}{l}{kx-y-k=0}\\{x+2y+4=0}\end{array}}\right.$,可得N坐标.再由两点间的距离公式化简得|AM|•|AN|.
解答 (1)解:圆心(3,4)到l1的距离$d=\frac{{|{2k-4}|}}{{\sqrt{1+{k^2}}}}<4$,
即$\frac{{2{k^2}-8k+8}}{{1+{k^2}}}<8$,解得$k>0或k<-\frac{4}{3}$.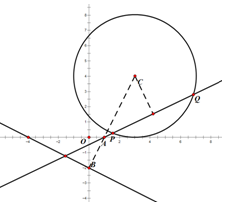
(2)证明:直线l1:kx-y-k=0恒过定点(1,0),
所以点A的坐标为(1,0),如图所示:将l1方程代入圆方程,
整理得(1+k)2x2-[6+2k(k+4)]•x+k2+8k+9=0.
由韦达定理和中点的坐标公式知:${x_M}=\frac{{{x_1}+{x_2}}}{2}=\frac{{3+k({k+4})}}{{1+{k^2}}}$,
因此,yM=$\frac{4{k}^{2}+2k}{1+{k}^{2}}$.
解方程组$\left\{{\begin{array}{l}{kx-y-k=0}\\{x+2y+4=0}\end{array}}\right.$,得$\left\{{\begin{array}{l}{x=\frac{2k-4}{2k+1}}\\{y=\frac{-5k}{2k+1}}\end{array}}\right.$,即$N({\frac{2k-4}{2k+1},\frac{-5k}{2k+1}})$.
再由两点间的距离公式化简得|AM|•|AN|=10.
点评 本题考查了直线与圆的方程、点到直线的距离公式、一元二次方程的根与系数的关系、中点坐标公式、两点之间的距离公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{2}$ | B. | x=0 | C. | x=-$\frac{π}{6}$ | D. | x=$\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2=8y | B. | y2=16x | C. | x2=-8y | D. | y2=-16x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 对此事的态度 | 好评(有利于百姓出行) | 中评(影响不大) | 差评(纯属忽悠) | 不关心 |
| 人数 | 2000 | 4000 | 3000 | 1000 |
| A. | 10 | B. | 8 | C. | 5 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{14}{13}$ | C. | $\frac{56}{41}$ | D. | $\frac{29}{23}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
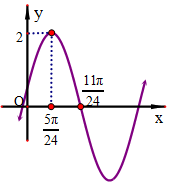 已知f(x)=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示,则y=f(x)+cos(ωx+$\frac{7π}{12}$)的增区间是[kπ-$\frac{7}{24}$π,kπ+$\frac{5π}{24}$],k∈Z.
已知f(x)=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示,则y=f(x)+cos(ωx+$\frac{7π}{12}$)的增区间是[kπ-$\frac{7}{24}$π,kπ+$\frac{5π}{24}$],k∈Z.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com