
【题目】![]() 是衡量空气污染程度的一个指标,为了了解
是衡量空气污染程度的一个指标,为了了解![]() 市空气质量情况,从
市空气质量情况,从![]() 年每天的
年每天的![]() 值的数据中随机抽取
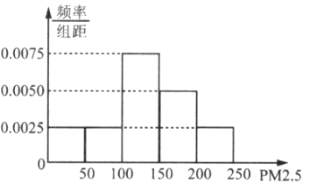
值的数据中随机抽取![]() 天的数据,其频率分布直方图如图所示.将
天的数据,其频率分布直方图如图所示.将![]() 值划分成区间
值划分成区间![]() 、
、![]() 、
、![]() 、
、![]() ,分别称为一级、二级、三级和四级,统计时用频率估计概率 .
,分别称为一级、二级、三级和四级,统计时用频率估计概率 .
(1)根据![]() 年的数据估计该市在
年的数据估计该市在![]() 年中空气质量为一级的天数;
年中空气质量为一级的天数;
(2)按照分层抽样的方法,从样本二级、三级、四级中抽取![]() 天的
天的![]() 数据,再从这
数据,再从这![]() 个数据中随机抽取
个数据中随机抽取![]() 个,求仅有二级天气的概率.
个,求仅有二级天气的概率.
【答案】(1)91天 (2) ![]()
【解析】
(1)由频率近似概率,计算空气质量为一级的天数即可;
(2)首先确定每组抽取的个数,然后列出所有可能的基本事件,并找到满足题意的事件,最后利用古典概型计算公式可得满足题意的概率值.
(1)由样本空气质量![]() 的数据的频率分布直方图可知,其频率分布如下表:
的数据的频率分布直方图可知,其频率分布如下表:
|
|
|
|
|
|
频率 |
|
|
|
|
|
由上表可知,如果![]() 市维持现状不变,那么该市
市维持现状不变,那么该市![]() 年的某一天空气质量为一级的概率为
年的某一天空气质量为一级的概率为![]() ,
,
因此在![]() 天中空气质量为一级的天数约有
天中空气质量为一级的天数约有![]() (天).
(天).
(2)在样本中,按照分层抽样的方法抽取![]() 天的
天的![]() 值数据,则这
值数据,则这![]() 个数据中二级、三级、四级天气的数据分别有
个数据中二级、三级、四级天气的数据分别有![]() 个、
个、![]() 个、
个、![]() 个.分别记为
个.分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,从这
,从这![]() 个数据中随机抽取
个数据中随机抽取![]() 个,基本事件为:
个,基本事件为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,共
,共![]() 个基本事件上,
个基本事件上,
事件![]() “仅有二级天气”包含
“仅有二级天气”包含![]() ,
,![]() ,
,![]() 3个基本事件,
3个基本事件,
故所求概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,以椭圆四个顶点为顶点的四边形的面积为
,以椭圆四个顶点为顶点的四边形的面积为![]() .
.
(1)求椭圆E的方程;
(2)过椭圆E的右焦点![]() 作直线
作直线![]() 与E交于A,B两点,O为坐标原点,求
与E交于A,B两点,O为坐标原点,求![]() 面积的最大值,并求此时直线
面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,过点
,过点![]() 作与
作与![]() 轴垂直的直线
轴垂直的直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点(点
两点(点![]() 在第一象限),过椭圆的左顶点和上顶点的直线
在第一象限),过椭圆的左顶点和上顶点的直线![]() 与直线
与直线![]() 交于
交于![]() 点,且满足
点,且满足![]() ,设
,设![]() 为坐标原点,若
为坐标原点,若![]() ,
,![]() ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解所经销商品的使用情况,随机问卷50名使用者,然后根据这50名的问卷评分数据,统计得到如图所示的频率布直方图,其统计数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求频率分布直方图中a的值并估计这50名使用者问卷评分数据的中位数;
(2)从评分在[40,60)的问卷者中,随机抽取2人,求此2人评分都在[50,60)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的单调区间;
的单调区间;
(3)是否存在整数![]() 使得函数
使得函数![]() 的极大值大于零,若存在,求
的极大值大于零,若存在,求![]() 的最小整数值,若不存在,说明理由.
的最小整数值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有红球3个、白球2个、黑球1个,从中任取2个,则互斥而不对立的两个事件是![]()
![]()
A. 至少有一个白球;都是白球 B. 至少有一个白球;至少有一个红球
C. 至少有一个白球;红、黑球各一个 D. 恰有一个白球;一个白球一个黑球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理是类比推理的( )
A. 两条直线平行,同旁内角互补,如果![]() 和
和![]() 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则![]()
B. 由平面三角形的性质,推测空间四边形的性质
C. 某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员.
D. 一切偶数都能被2整除,![]() 是偶数,所以
是偶数,所以![]() 能被2整除.
能被2整除.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年11月3日20点43分我国长征运载火箭在海南文昌发射中心成功发射,它被公认为我国已从航天大国向航天强国迈进的重要标志.长征五号运载火箭的设计生产采用很多新材料,甲工厂承担了某种材料的生产,并以![]() 千克/时的速度匀速生产(为保证质量要求
千克/时的速度匀速生产(为保证质量要求![]() ),每小时可消耗
),每小时可消耗![]() 材料
材料![]() 千克,已知每小时生产1千克该产品时,消耗
千克,已知每小时生产1千克该产品时,消耗![]() 材料10千克.
材料10千克.
(1)设生产![]() 千克该产品,消耗
千克该产品,消耗![]() 材料
材料![]() 千克,试把
千克,试把![]() 表示为
表示为![]() 的函数.
的函数.
(2)要使生产1000千克该产品消耗的![]() 材料最少,工厂应选取何种生产速度?并求消耗的
材料最少,工厂应选取何种生产速度?并求消耗的![]() 材料最少为多少?
材料最少为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com