
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,其中
是直角梯形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 上的点,且
上的点,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)设![]() 为棱
为棱![]() 上的点(不与
上的点(不与![]() ,
,![]() 重合),且直线
重合),且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)建立适当的空间直角坐标系,确定各点坐标,得到![]() ,
,![]() ,根据线面垂直的判定定理,即可证明.
,根据线面垂直的判定定理,即可证明.
(2)由(1)可知,平面![]() 的法向量
的法向量![]() ,确定平面
,确定平面![]() 的法向量
的法向量![]() ,根据
,根据 ,求解即可.
,求解即可.
(3)设![]() ,确定
,确定![]() ,
,![]() ,根据直线
,根据直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求解
,求解![]() ,即可.
,即可.
(1)因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() ,
,![]()
因为![]()
则以A为坐标原点,建立如图所示的空间直角坐标系.
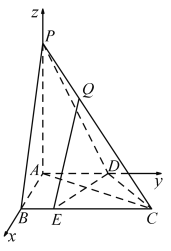
由已知可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
因为![]() ,
,![]() .
.
所以![]() ,
,![]()
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
所以![]() 平面
平面![]() .
.
(2)设平面![]() 的法向量
的法向量![]() ,由(1)可知,
,由(1)可知,![]()
设平面![]() 的法向量
的法向量![]()
因为![]() ,
,![]() .
.
所以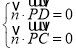 ,即
,即![]()
不妨设![]() ,得
,得![]() .
.
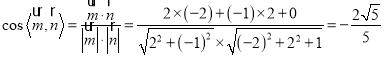
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(3)设![]() ,即
,即![]() .
.
所以![]() ,即
,即![]() .
.
因为直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()
所以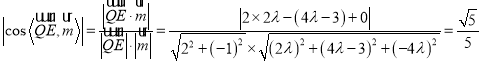
即![]() 解得
解得![]()
即![]() .
.


科目:高中数学 来源: 题型:
【题目】为了预防流感,某学校对教室用药熏消毒法进行消毒,已知药物释放过程中,室内每立方米空气中的含药量![]() 与时间
与时间![]() 成正比,药物释放完毕后,
成正比,药物释放完毕后,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数).如图所示,根据图中提供的信息,回答下列问题:
为常数).如图所示,根据图中提供的信息,回答下列问题:
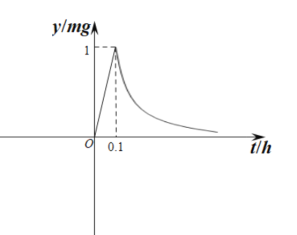
(1)从药物释放开始,每立方米空气中的含药量![]() 与时间
与时间![]() 之间的函数关系式为________;
之间的函数关系式为________;
(2)据测定,当空气中每立方米的含药量降低到![]() 以下时,学生方可进教室,那么从药物释放开始,至少需要经过多少时间学生才能回到教室?
以下时,学生方可进教室,那么从药物释放开始,至少需要经过多少时间学生才能回到教室?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:y=x+m,m∈R.
(I)若以点M(2,0)为圆心的圆与直线l相切与点P,且点P在y轴上,求该圆的方程;
(II)若直线l关于x轴对称的直线为![]() ,问直线
,问直线![]() 与抛物线C:x2=4y是否相切?说明理由.
与抛物线C:x2=4y是否相切?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知双曲线![]() .
.
(1)过![]() 的左顶点引
的左顶点引![]() 的一条渐近线的平行线,求该直线与另一条渐近线及x轴围成的三角形的面积;
的一条渐近线的平行线,求该直线与另一条渐近线及x轴围成的三角形的面积;
(2)设斜率为1的直线l交![]() 于P,Q两点,若l与圆
于P,Q两点,若l与圆![]() 相切,求证:
相切,求证:![]() ;
;
(3)设椭圆![]() ,若M,N分别是
,若M,N分别是![]() ,
,![]() 上的动点,且
上的动点,且![]() ,求证:O到直线MN的距离是定值.
,求证:O到直线MN的距离是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 和圆
和圆![]() ,倾斜角为45°的直线
,倾斜角为45°的直线![]() 过抛物线
过抛物线![]() 的焦点,且
的焦点,且![]() 与圆
与圆![]() 相切.
相切.
(1)求![]() 的值;
的值;
(2)动点![]() 在抛物线
在抛物线![]() 的准线上,动点
的准线上,动点![]() 在
在![]() 上,若
上,若![]() 在
在![]() 点处的切线
点处的切线![]() 交
交![]() 轴于点
轴于点![]() ,设
,设![]() .求证点
.求证点![]() 在定直线上,并求该定直线的方程.
在定直线上,并求该定直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
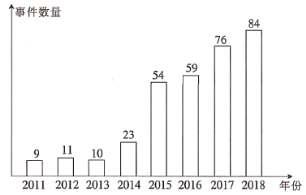
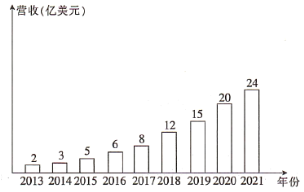
【题目】随着社会的发展与进步,传播和存储状态已全面进入数字时代,以数字格式存储,以互联网为平台进行传输的音乐——数字音乐已然融入了我们的日常生活.虽然我国音乐相关市场仍处在起步阶段,但政策利好使音乐产业逐渐得到资本市场更多的关注.对比如下两幅统计图,下列说法正确的是( )
2011-2018年中国音乐产业投融资事件数量统计图
2013-2021年中国录制音乐营收变化及趋势预测统计图
A.2011~2018年我国音乐产业投融资事件数量逐年增长
B.2013~2018年我国录制音乐营收与音乐产业投融资事件数量呈正相关关系
C.2016年我国音乐产业投融资事件的平均营收约为![]() 亿美元
亿美元
D.2013~2019年我国录制音乐营收年增长率最大的是2018年
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com