
【题目】如图,在三棱柱![]() 中,
中, ![]() ,
, ![]() 平面
平面![]() ,侧面
,侧面![]() 是正方形,点
是正方形,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 、
、![]() 分别在棱
分别在棱![]() 、
、![]() 上,且
上,且![]() ,
, ![]() .
.
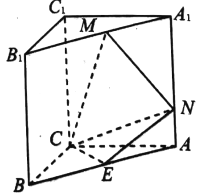
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=![]() ,AC=3, BC=2,P是△ABC内的一点.
,AC=3, BC=2,P是△ABC内的一点.

(1)若△BPC是以BC为斜边的等腰直角三角形,求PA长;
(2)若∠BPC=![]() ,求△PBC面积的最大值.
,求△PBC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() +
+![]() =1的左焦点为F,直线x-y-2=0,x-y+2=0与椭圆分别相交于A,B,C,D,则|AF|+|BF|+|CF|+|DF|=______.
=1的左焦点为F,直线x-y-2=0,x-y+2=0与椭圆分别相交于A,B,C,D,则|AF|+|BF|+|CF|+|DF|=______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王想进行理财投资,根据长期收益率市场顶测,投资A类产品和B类产品的收益分别为![]() (万元),它们与投资额x(万元)存在如下关系式:
(万元),它们与投资额x(万元)存在如下关系式:![]() ,
,![]() ,小王准备将200万元资金投入A、B两类理财产品,公司要求每类产品的投资金额不能低于25万元
,小王准备将200万元资金投入A、B两类理财产品,公司要求每类产品的投资金额不能低于25万元
(1)若对B类产品的投资金额为x(万元),求总收益y(万元)关于x的函数关系式;
(2)请你帮助小王预算如何分配投资资金,才能使总收益最大,并求出最大总收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的公差d>0,则下列四个命题:
的公差d>0,则下列四个命题:
①数列![]() 是递增数列; ②数列
是递增数列; ②数列![]() 是递增数列;
是递增数列;
③数列![]() 是递增数列; ④数列
是递增数列; ④数列![]() 是递增数列.
是递增数列.
其中正确命题的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax-2|+lnx(其中a为常数)
(1)若a=0,求函数g(x)=![]() 的极值;
的极值;
(2)求函数f(x)的单调区间;
(3)令F(x)=f(x)-![]() ,当a≥2时,判断函数F(x)在(0,1]上零点的个数,并说明理由.
,当a≥2时,判断函数F(x)在(0,1]上零点的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年中央电视台春节联欢晚会分会场之一落户黔东南州黎平县肇兴侗寨,黔东南州某中学高二社会实践小组就社区群众春晚节目的关注度进行了调查,随机抽取80名群众进行调查,将他们的年龄分成6段: ![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
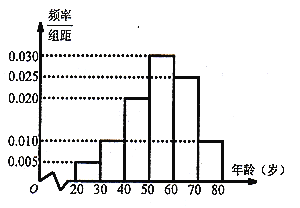
, ![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
(Ⅰ)求这80名群众年龄的中位数;
(Ⅱ)将频率视为概率,现用随机抽样方法从该社区群众中每次抽取1人,共抽取3次,记被抽取的3人中年龄在![]() 的人数为
的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列,及数学期望
的分布列,及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 也为抛物线
也为抛物线![]() 的焦点.(1)若
的焦点.(1)若![]() 为椭圆
为椭圆![]() 上两点,且线段
上两点,且线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)若过椭圆![]() 的右焦点
的右焦点![]() 作两条互相垂直的直线分别交椭圆于
作两条互相垂直的直线分别交椭圆于![]() 和
和![]() ,设线段
,设线段![]() 的长分别为
的长分别为![]() ,证明
,证明![]() 是定值.
是定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com