小张在淘宝网上开一家商店,他以10元每条的价格购进某品牌积压围巾2000条.定价前,小张先搜索了淘宝网上的其它网店,发现:A商店以30元每条的价格销售,平均每日销售量为10条;B商店以25元每条的价格销售,平均每日销售量为20条.假定这种围巾的销售量t(条)是售价x(元)(x∈Z+)的一次函数,且各个商店间的售价、销售量等方面不会互相影响.
(1)试写出围巾销售每日的毛利润y(元)关于售价x(元)(x∈Z+)的函数关系式(不必写出定义域),并帮助小张定价,使得每日的毛利润最高(每日的毛利润为每日卖出商品的进货价与销售价之间的差价);
(2)考虑到这批围巾的管理、仓储等费用为200元/天(只要围巾没有售完,均须支付200元/天,管理、仓储等费用与围巾数量无关),试问小张应该如何定价,使这批围巾的总利润最高(总利润=总毛利润-总管理、仓储等费用)?
解:设t=kx+b,∴
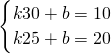
,解得k=-2,b=70,∴t=70-2x.…1分
(1)y=(x-10)•t=(x-10)•(70-2x)=-2x
2+90x-700,…1分
∵
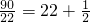
,∴围巾定价为22元或23元时,每日的利润最高.…2分
(2)设售价x(元)时总利润为z(元),
∴z=2000•(x-10)-200•
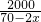
…1分
=2000•(25-((35-x)+
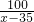
))≤2000•(25-
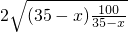
)=10000元.…1分
当35-x=
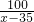
时,即x=25时,取得等号.…1分
∴小张的这批围巾定价为25元时,这批围巾的总利润最高.…1分.
分析:(1)根据题意先求出销售量t与售价x之间的关系式,再利用毛利润为每日卖出商品的进货价与销售价之间的差价,确定毛利润y(元)关于售价x(元)(x∈Z
+)的函数关系式,利用二次函数求最值的方法可求;
(2)根据总利润=总毛利润-总管理、仓储等费用,构建函数关系,利用基本不等式可求最值.
点评:本题以实际问题为载体,考查二次函数模型的构建,考查配方法求最值及基本不等式求最值,关键是函数式的构建.

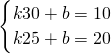 ,解得k=-2,b=70,∴t=70-2x.…1分
,解得k=-2,b=70,∴t=70-2x.…1分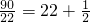 ,∴围巾定价为22元或23元时,每日的利润最高.…2分
,∴围巾定价为22元或23元时,每日的利润最高.…2分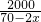 …1分
…1分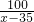 ))≤2000•(25-
))≤2000•(25-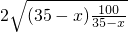 )=10000元.…1分
)=10000元.…1分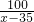 时,即x=25时,取得等号.…1分
时,即x=25时,取得等号.…1分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案