
【题目】若定义在![]() 上的函数
上的函数![]() ,
,![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() 、
、![]() 、
、![]() 满足
满足![]() ,则称
,则称![]() 比
比![]() 更接近
更接近![]() .当
.当![]() ,试比较
,试比较![]() 和
和![]() 哪个更接近
哪个更接近![]() ,并说明理由.
,并说明理由.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知直线l的参数方程为: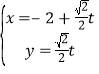 ,
,![]() 为参数
为参数![]() 点的极坐标为
点的极坐标为![]() ,曲线C的极坐标方程为
,曲线C的极坐标方程为![]() .
.
![]() Ⅰ
Ⅰ![]() 试将曲线C的极坐标方程化为直角坐标方程,并求曲线C的焦点在直角坐标系下的坐标;
试将曲线C的极坐标方程化为直角坐标方程,并求曲线C的焦点在直角坐标系下的坐标;
![]() Ⅱ
Ⅱ![]() 设直线l与曲线C相交于两点A,B,点M为AB的中点,求
设直线l与曲线C相交于两点A,B,点M为AB的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,南宁大力实施“二产补短板、三产强优势、一产显特色”策略,着力发展实体经济,工业取得突飞猛进的发展.逐步形成了以电子信息、机械装备、食品制糖、铝深加工等为主的4大支柱产业.广西洋浦南华糖业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如下表所示,已知
,如下表所示,已知![]() .
.

(1)求出q的值;
(2)已知变量x,y具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程![]() ;
;
(3)用![]() 表示用(2)中所求的线性回归方程得到的与
表示用(2)中所求的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数
称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数![]() 的数学期望Eξ.
的数学期望Eξ.
(参考公式:线性回归方程中![]() 的最小二乘估计分别为:
的最小二乘估计分别为: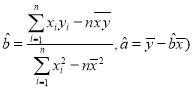
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面是等腰梯形,
的底面是等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为等边三角形,且点P在底面
为等边三角形,且点P在底面![]() 上的射影为
上的射影为![]() 的中点G,点E在线段
的中点G,点E在线段![]() 上,且
上,且![]() .
.
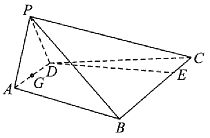
(1)求证:![]() 平面
平面![]() .
.
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂采用甲、乙两种不同生产方式生产某零件,现对两种生产方式所生产的这种零件的产品质量进行对比,其质量按测试指标可划分为:指标在区间![]() 100的为一等品;指标在区间
100的为一等品;指标在区间![]() 的为二等品
的为二等品![]() 现分别从甲、乙两种不同生产方式所生产的零件中,各自随机抽取100件作为样本进行检测,测试指标结果的频率分布直方图如图所示:
现分别从甲、乙两种不同生产方式所生产的零件中,各自随机抽取100件作为样本进行检测,测试指标结果的频率分布直方图如图所示:

![]() 若在甲种生产方式生产的这100件零件中按等级,利用分层抽样的方法抽取10件,再从这10件零件中随机抽取3件,求至少有1件一等品的概率;
若在甲种生产方式生产的这100件零件中按等级,利用分层抽样的方法抽取10件,再从这10件零件中随机抽取3件,求至少有1件一等品的概率;
![]() 将频率分布直方图中的频率视作概率,用样本估计总体
将频率分布直方图中的频率视作概率,用样本估计总体![]() 若从该厂采用乙种生产方式所生产的所有这种零件中随机抽取3件,记3件零件中所含一等品的件数为X,求X的分布列及数学期望.
若从该厂采用乙种生产方式所生产的所有这种零件中随机抽取3件,记3件零件中所含一等品的件数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)设函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)如果对所有的![]() ≥0,都有
≥0,都有![]() ≤
≤![]() ,求
,求![]() 的最小值;
的最小值;
(Ⅲ)已知数列![]() 中,
中, ![]() ,且
,且![]() ,若数列
,若数列![]() 的前n项和为
的前n项和为![]() ,求证:
,求证:
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com