
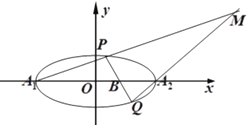
【题目】如图,已知椭圆![]() 的右准线
的右准线![]() 的方程为
的方程为![]() ,焦距为
,焦距为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过定点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (异于椭圆
(异于椭圆![]() 的左、右顶点
的左、右顶点![]() )两点,设直线
)两点,设直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
①若![]() ,试求点
,试求点![]() 的坐标;
的坐标;
②求证:点![]() 始终在一条直线上.
始终在一条直线上.
【答案】(1)点![]() 的坐标为
的坐标为![]() ,
, ![]() 的坐标为
的坐标为![]() (2)见解析.
(2)见解析.
【解析】试题分析:(1)由椭圆的离心率公式和a,b,c的关系,解方程可得a,b,进而得到椭圆方程;(2)①求得直线MA1的方程和以MA2的方程,代入椭圆方程,求得交点P,Q的坐标;②设点M(x0,y0),求得直线MA1的方程和以MA2的方程,代入椭圆方程,求得交点P,Q的坐标,结合P,Q,B三点共线,所以kPB=kQB,化简整理,可得![]() 或
或![]() .分别考虑,即可得到点M始终在一条定直线x=4上.
.分别考虑,即可得到点M始终在一条定直线x=4上.
试题解析:
⑴由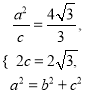 得
得![]() 所以椭圆
所以椭圆![]() 的方程为
的方程为![]() .
.
⑵①因为![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() 的方程为
的方程为![]() ,代入
,代入![]() ,
,
![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,则
,则![]() ,所以点
,所以点![]() 的坐标为
的坐标为![]() .
.
同理可得点![]() 的坐标为
的坐标为![]() .
.
②设点![]() ,由题意,
,由题意, ![]() .因为
.因为![]() ,
, ![]() , 所以直线
, 所以直线![]() 的方程为
的方程为![]() ,代入
,代入![]() ,得
,得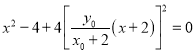 ,
,
即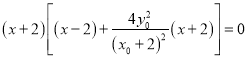 ,因为
,因为![]() ,
,
所以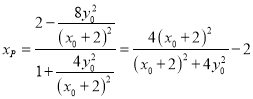 ,则
,则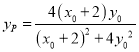 ,故点
,故点![]() 的坐标为
的坐标为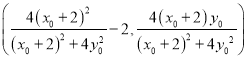 .
.
同理可得点![]() 的坐标为
的坐标为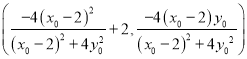 .
.
因为![]() ,
, ![]() ,
, ![]() 三点共线,所以
三点共线,所以![]() ,
, ![]() .
.
所以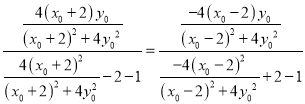 ,即
,即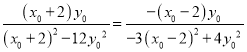 ,
,
由题意, ![]() ,所以
,所以![]() .
.
即![]() .
.
所以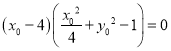 ,则
,则![]() 或
或![]() .若
.若![]() ,则点
,则点![]() 在椭圆上,
在椭圆上, ![]() ,
, ![]() ,
, ![]() 为同一点,不合题意.故
为同一点,不合题意.故![]() ,即点
,即点![]() 始终在定直线
始终在定直线![]() 上.
上.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+5﹣a|
(1)若不等式f(x)﹣|x﹣a|≤2的解集为[﹣5,﹣1],求实数a的值;
(2)若x0∈R,使得f(x0)<4m+m2 , 求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和是Sn,且Sn![]() =1(n∈N),数列{bn}是公差d不等于0的等差数列,且满足:b1=
=1(n∈N),数列{bn}是公差d不等于0的等差数列,且满足:b1=![]() ,而b2,b5,ba14成等比数列.
,而b2,b5,ba14成等比数列.
(1)求数列{an}、{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校高一年级研究性学习小组共有9名学生,其中有3名男生和6名女生.在研究性学习过程中,要进行两次汇报活动(即开题汇报和结题汇报),每次汇报都从这9名学生中随机选1 人作为代表发言.设每人每次被选中与否均互不影响.
(1)求两次汇报活动都由小组成员甲发言的概率;
(2)设![]() 为男生发言次数与女生发言次数之差的绝对值,求
为男生发言次数与女生发言次数之差的绝对值,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(![]() )若关于
)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
(![]() )若关于
)若关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ,求
,求![]() ,
,![]() 的值.
的值.
(![]() )若关于
)若关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ,集合
,集合![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】矩形![]() 中,
中, ![]() ,
, ![]() 边所在直线的方程为
边所在直线的方程为![]() ,点
,点![]() 在
在![]() 边所在直线上.
边所在直线上.
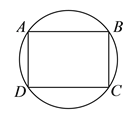
(![]() )求
)求![]() 边所在直线的方程.
边所在直线的方程.
(![]() )求矩形
)求矩形![]() 外接圆的方程.
外接圆的方程.
(![]() )若过点
)若过点![]() 作题(
作题(![]() )中的圆的切线,求切线的方程.
)中的圆的切线,求切线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com